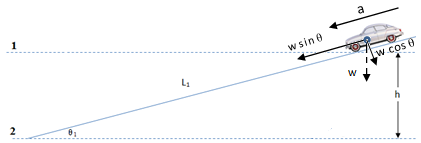اختبر معلوماتك عن السيارات

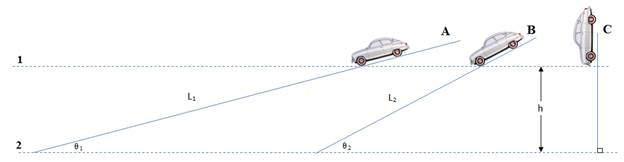
1- حركة السيارة على مستوى مائل هبوطا:

نطرح السؤال التالي لكي تكون الإجابة عليه توضيح لحركة السيارة هبوطا على مستوى مائل.

السيارة متوقفة على الطريق المائل في الوضع 1 (المحرك لا يعمل, ناقل الحركة في وضع الحياد, فرملة اليد مرفوعة).

الحالة الأولى: السيارة متوقفة على الطريق المائل A (أقل ميل/انحدار)

الحالة الثانية: نفس السيارة متوقفة على الطريق المائل B (أكثر ميل/انحدار)

تم عتق/ تنزيل فرامل اليد, وبدأت السيارة الحركة لأسفل تحت تأثير الجاذبية الأرضية فقط من الوضع 1, ونفترض أن المسافة الرأسية التي ستهبطها السيارة هي (h) لتصل إلى الوضع 2:

وعند الوضع 2 تم تسجيل سرعة السيارة

* أي الحالتين ستكون عندها تكون السيارة أسرع عند الوصول للوضع 2 ؟

أ- عند تدحرجها نزولا على الميل A

ب- عند تدحرجها نزولا على الميل  B

جـ- السيارة سيكون لها نفس السرعة على أي من الميلين (A أو B)

V

V

V

لجعل السؤال أكثر تشويقا, سنضيف الحالة الثالثة C, سقوط السيارة رأسيا من الوضع 1 إلى 2

* تم تسجيل سرعة السيارة وزمن الوصول, ومعدل زيادة السرعة في الثلاث حالات

ونكرر السؤال مرة أخرى: في أي الحالات تكون السيارة أسرع عند المستوى 2؟

أ- ستكون السيارة أسرع عند نزولها الميل A

ب- ستكون السيارة أسرع عند نزولها الميل B

جـ- ستكون السيارة أسرع عند نزولها الميل C (رأسيا لأسفل)

د- السيارة سيكون لها نفس السرعة في أي من الحالات بما في ذلك الحالة C

V

V

V

يعتقد كثيرا من الناس أن الإجابة على السؤال السابق هو الاختيار جـ, فهل توافق على ذلك؟

V

V

V

لتسهيل الاجابة (أهمل قيمة مقاومات الحركة للسيارة في جميع الحالات)

V

V

V

الإجابة هي:

السيارة عند هبوطها على أي مستوى سيكون لها نفس السرعة, الاختيار (د)

أي أن سرعة السيارة عند الوضع 2 في: الحالة A =  الحالة B = الحالة C

V

V

V

الاجابة تحتاج إلى تفسير وإثبات, بالإضافة إلى مزيد من القياسات

تم قياس زمن الوصول, وكذلك معدل تزايد السرعة من الوضع 1 إلى الوضع 2

دراسة الابعاد هندسيا ومعادلات الحركة للسيارة:

من دراسة طاقة السيارة:

# (بالنسبة للأشخاص الغير معجبين بالمعادلات يمكن التركيز على العبارات باللون الأخضر, وتجنب التحليل والمعادلات, والرقم بين القوسين يدل على رقم المعادلة):

عندما تكون السيارة في الوضع 1 فإنها تزيد طاقتها (طاقة الوضع) عن وضعها في الوضع 2 بمقدار وزن الجسم في المسافة الرأسية بين الوضعين

PE = w h

حيث

PE =] [فرق طاقة الوضع للسيارة في الوضع 1 عن  الوضع 2

h =]  [ارتفاع (المسافة الرأسية) بين الوضع 1 والوضع 2

w = وزن السيارة = m g =] [كتلة السيارة × في عجلة الجاذبية

هذه الطاقة تتحول إلى طاقة حركة بالكامل (مع إهمال الشغل الضائع في المقاومات)

w h = ½ m v²  = [نصف كتلة السيارة × مربع سرعة السيارة]

حيث

كتلة السيارة  = m

)سرعة السيارة عند الوضع 2( = v

فتكون المعادلة

w h = (m g) h = ½ m v²

وعليه فتكون:

v² = 2 g h

v = √ (2 g h) ……………………………(1)

(1).... سرعة السيارة في الوضع 2 تزيد مع زيادة الارتفاع الرأسي للمنحدر (h)
ولا تعتمد على ميل المنحدر (θ), وعلى الكتلة (m) أو الوزن.  

من المعادلة الأولى (1) يتضح أن سرعة السيارة عند وصولها عند الوضع 2 بداية من السكون في الوضع 1 تكون متساوية في أي حالة. وستظل لها نفس القيمة على أي منحدر(مع تغير المقدار) في زيادة المسافة الرأسية h بين الوضع 1 والوضع 2 (تزيد السرعة في جميع الحالات مع زيادة المسافة الرأسية) لا يؤثر الميل على سرعة السيارة. وهذه حالة عامة يمكن تطبيقها على أي سيارة مع اختلاف كتلتها حيث لا يوجد كتلة السيارة m بالمعادلة.

* إذا السرعة عند الوضع 2 لكل الحالات A, B, C  ستكون متساوية  [v_A= v_B = v_C]₂

V

V

V

وهنا قد تدور في رأسك بعض الاسئلة ؟؟؟؟؟؟

- من المعادلات نجد أن سرعة أي سيارة ستكون متساوية عند هبوطها لأي مسافة رأسية على أي ميل للطريق؟

= صح

- هذا غير منطقي يجب أن يكون هناك شيء مختلف؟

= نعم هناك شيء مختلف, ولذلك سنقوم باستكمال الدراسة:

من دراسة العلاقة الهندسية لميل المنحني:

يمثل الميل الشكل الهندسي (مثلث قائم الزاوية), الضلع الرأسي الارتفاع h, والوتر المسافة التي تقطعها السيارة (L), والضلع الأفقي المسافة الأفقية التي ستقطعها السيارة.

sin θ = h / L

L = h/sin θ …………………………….(2)

(2)...  المسافة المقطوعة على المنحدر تزيد مع قلة الميل (θ) وتعتمد على الارتفاع الرأسي للمنحدر (h)

من دراسة حركة السيارة:

القوى المؤثرة على السيارة تعمل على التغلب على المقاومات, وإكساب السيارة زيادة في السرعة

القوة المؤثرة عليها في اتجاه الحركة = كتلة السيارة × تعجيل السيارة

w sin θ = m a

m g sin θ = m a

a = g sin θ ………………………………(3)

(3)... تعجيل السيارة (معدل زيادة سرعة) أثناء نزولها على منحدر يزيد مع زيادة ميل المنحنى (θ), القيمة القصوى لها تكون في حالة سقوط السيارة وتساوي عجلة الجاذبية الأرضية g.

مع تطبيق معادلات الحركة:

v = v_o + a t

√ (2 g h) = 0 + (g sin θ) t

t = [√ (2 g h)] / (g sin θ) …………………(4)

(4)... زمن هبوط السيارة للوضع 2 يزيد مع قلة المنحدر (θ) ويعتمد على الارتفاع الرأسي للمنحدر (h)

* كلما تغير الميل, ستتغير المسافة التي ستقطعها السيارة هبوطا على الطريق وعليه سيختلف زمن هبوط السيارة لوصولها من الوضع 1 إلى الوضع 2.

* كلما قل الميل كلما زادت المسافة المقطوعة والزمن (السيارة ستصل إلى الوضع 2؛ في الحالة C أسرع من الحالة B والحالة A), كما ستقطع مسافة أقل هبوطا.

* وحيث أن الزمن سيزيد كلما قل الميل فإن معدل تغيير السرعة (التغير في السرعة بالنسبة للزمن) (العجلة acceleration) ستقل كما قل الميل. أي أن السيارة ستزداد سرعتها ببطء على الميل A  حتى تصل إلى السرعة v, عنها عن B  و C.

مثال توضيحي: مع فرض قيم لزاوية ميل المنحدر (θ), وفرض قيمة للارتفاع الرأسي h = 3 m, وقيمة عجلة الجاذبية g = 9.81 m/s^2
حالة السيارة عند الوضع 2			90^o	45^o	30^o
السرعة ............(1)	v	√(2 g h)	7.672 م/ث 27.62 كم/ساعة	7.672 م/ث 27.62 كم/ساعة	7.672 م/ث 27.62 كم/ساعة
المسافة المقطوعة من الحالة 1- 2 .......(2)	L	h /sin θ	3 متر	4.24 متر	6 متر
تعجيل السرعة .. (3)	a	g sin θ	9.81 م/ ث^2 ^(9.81 متر/ثانية) كل ثانية	6.937 م/ ث^2 ^(6.937 متر/ثانية) كل ثانية	4.905 م/ ث^2 ^(4.905 متر/ثانية) كل ثانية
زمن الوصول من الحالة 1- 2 ...... (5)	t	[√(2 g h)] /(g sin θ)	0.782  ثانية	1.106 ثانية	1.564 ثانية

في حالة اهمال المقاومات

السرعة لا تعتمد على كتلة أو وزن السيارة

كما يتضح أن جميع المتغيرات (السرعة, زمن الوصول, التعجيل) لا تعتمد على كتلة السيارة m, أو الوزن w,

وعليه فالنتيجة واحدة عند إجراء المقارنة على أي نوع أو شكل أو وزن للسيارة لمسافات رأسية محدودة.

ولكن ماذا في حالة عدم إهمال المقاومات؟

في حالة عدم اهمال المقاومات فإن الشغل الميكانيكي W الناجم من حركة السيارة يساوي قوة المقاومة في المسافة W = F x L, وحيث أن مقاومة التدحرج F = RR = f_r x w cos ɵ أعلى في الحالة A (كلما قلت الزاوية, كلما زادت المركبة الرئيسية للوزن), بالإضافة إلى أن المسافة المقطوعة L = h / sin ɵ أطول في الحالة A, فأن ذلك سوف يقلل من مقدار الطاقة وعليه فإن سرعة السيارة في الحالة B ستكون أسرع, والحالة C ستكون أكثر سرعة منهما.

f_r = معامل التدحرج, وهو ثابت تقريبا من الناحية العلمية, ويعتمد على نوع الإطار, والطريق, وضغط نفخ الهواء. وقد يتأثر طفيفا بانبعاج الإطار نتيجة الحمل الواقع على الإطار والذي يهمل في التطبيقات العملية.

w = وزن السيارة , والذي هو يساوي كتلة الجسم m مضروب في عجل الجاذبية الأرضية g. w = mg

cos ɵ = جيب تمام زاوية الميل, وهي تساوي المسافة الأفقية مقسومة على طول الوتر. ومقدارها يقل مع زيادة الزاوية.

sin ɵ = جيب زاوية الميل, وهي تساوي المسافة الرأسية مقسومة على طول الوتر. ومقدارها يقل مع قلة الزاوية.