معلومات السيارات

2- حركة السيارة على مستوى مائل هبوطا

لتوضيح حركة السيارة هبوطا على مستوى مائل نطرح السؤال التالي:

- في حالة هبوط سيارتين على نفس المستوى المائل لأسفل تحت تأثير وزنهما فقط, سيارة كبيرة ثقيلة الوزن, وسيارة صغيرة خفيفة الوزن أيهما تعتقد ستصل إلى اسفل الطريق المنحدر أولا (في حالة بدأهما من نفس النقطة على الطريق) ؟

لتسهيل السؤال السابق سنستخدم نفس السيارة في حالتين مختلفتين:

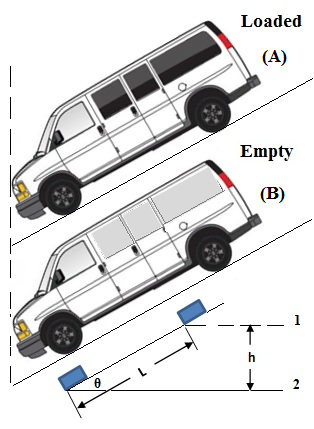
الحالة (A) نقوم بتحميل السيارة مما سيؤدي إلى زيادة وزنها,

الحالة (B) السيارة فارغة بدون حمولة, وزن أقل للسيارة عن الحالة السابقة:

نفس السيارة تعني (نفس الأجزاء الميكانيكية, الشكل والأبعاد الخارجية) ونعيد السؤال مرة أخرى:

- في حالة هبوط سيارة على طريق منحدر من نقطة (1) على الطريق وصولا إلى نقطة (2) اسفل الطريق تحت تأثير وزنها فقط (مع اهمال المقاومات):

هل

أ- السيارة وهي محملة في الحالة (A) ستصل في وقت أسرع

ب- السيارة وهي غير محملة (فارغة) في الحالة (B) ستصل في وقت أسرع

جـ- السيارة ستستغرق نفس الوقت للوصول إلى نهاية الميل في كلا الحالتين (A) و (B)

V

V

V

لتسهيل الحل إليك هذا المثال الاكثر سهولة

في حالة اسقاط كرتين من مكان مرتفع (كرة كتلتها 10 كيلوجرام, وكرة كتلتها 1 كيلوجرام) من نفس الارتفاع أيهما ستصل إلى الأرض أولا (10 كيلوجرام أم 1 كيلوجرام)؟

V

V

V

اعتقد الناس لفترة طويلة أن الكرة الثقيلة ستسقط أسرع, وهو ما كان أرسطو Aristotle يدرسه لطلبته: في حالة سقوط جسمين مختلفي الكتلة فإن الجسم ذو الكتلة الأكبر سيصل إلى الأرض أولا

V

V

V

هل هذا يساعدك في الحل؟

V

V

V

في القرن 17 قام العالم الإيطالي جاليليو جاليلي Galileo Galilei العالم الإيطالي بطرح نظرية جديدة: بأن الجسمين سيصلان الأرض في نفس الوقت,

وقد قام بتجربة بإسقاط جسمين مختلفين من قمة برج بيزا, ودحض بذلك نظرية أرسطو *

* في أواخر 1500, كان الناس تعتقد أن الجسم الأثقل يهبط أسرع من الجسم الأخف وزنا. كما كان معروف من أيام أرسطو. ويعزى إلى جاليلو جاليلي الذي كان يشغل منصب استاذ رياضيات في جامعة بيزا بدحض هذا الاعتقاد, حيث يقال أنه قام بأسقاط جسمين مختلفين الوزن (الكتلة) من برج بيزا المائل حيث برهن على سقوطهما في نفس الزمن. أدى تحديه لمعتقدات أرسطو أن فقد منصبه بالجامعة جراء ذلك.

في عام 1971 خلال رحلة أبولو 15 قام رائد الفضاء الأمريكي بإجراء التجربة بأسقاط ريشة و مطرقة على سطح القمر (في عدم وجود مقاومة للهواء) وعضد نظرية جاليليو

هل هناك علاقة بين الاسئلة الخاصة بهبوط السيارة بكتلة مختلفة على مستوى مائل والمثال؟ أم ان هذا المثال ليس له علاقة بالأسئلة السابقة

V

V

V

نعم؛ يوجد علاقة بين سقوط الجسم والهبوط على مستوى مائل بالنسبة لمعدل تعجيل السرعة (العجلة)

هبوط رأسي	هبوط على مستوى مائل
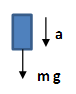
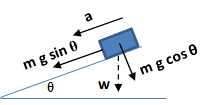
m g = m a a = g	m g sin θ = m a a = g sin θ
معدل تزايد سرعة الجسم a لا يعتمد على كتلة أو وزن الجسم أنما يساوي عجلة الجاذبية الأرضية في جيب زاوية الميل, وتساوي القيمة القصوى لها: عجلة الجاذبية الأرضية g في حالة السقوط الرأسي (Sin 90^o = 1).

وماذا عن السيارة

V

بتطبيق معادلات الحركة:

واخذ في الاعتبار أن عجلة (تسارع) السيارة متساوية في الحالتين ويساوي

a = g sin θ  ………………………….………………….(1)

وعليه فتكون السرعة

v² = v_o² + 2 a s = 0 + 2 a L

حيث السرعة الابتدائية v_o = 0 (الإنطلاق من السكون)

v = √ (2 a L)  ……………………………………………(2)

- حيث أن الميل واحد في الحالتين: يكون طول المسار متساوي L, وأن التعجيل a يعتمد على الميل ومتساوي في الحالتين, فإن سرعة السيارة في الحالتين ستكون متساوية عند الوصول إلى اسفل المنحدر ولا تعمد على وزن السيارة

وكذلك بالنسبة لزمن الوصول

v = v_o + a t = 0 + a t

وعليه فيكون زمن الوصول

t = v/a = (√ (2 a L))/a =√(2 L/a) ………………………(3)

- حيث أن الميل واحد في الحالتين: يكون طول المسار متساوي L, وأن التعجيل a يعتمد على الميل ومتساوي في الحالتين, فإن زمن وصول السيارة في الحالتين ستكون متساوية عند الوصول إلى اسفل المنحدر ولا تعمد على وزن السيارة

مما سبق يتضح أنه في حالة اهمال المقاومات وهبوط سيارة على أي منحدر (بطول L) في حالتين مختلفتين, حالة A وهي محملة, وحالة B وهي فارغة فأن:

- سرعة وصول السيارة (v) في الحالتين (A), (B) أسفل المنحدر ستكون واحدة ولا تعتمد على كتلة أو وزن السيارة

- زمن وصول السيارة (t) في الحالتين (A), (B) أسفل المنحدر ستكون واحدة ولا تعتمد على كتلة أو وزن السيارة

ماذا عن الحالة الفعلية؟ أذا أردت أن تعرف.....

مقاومة الحركة	مقاومة الهواء, مقاومة التدحرج
الحالة	حالة سقوط الجسم (مقاومة هواء فقط)	حالة السيارة على منحدر (أهمال مقاومة الهواء عند السرعات المنخفضة, مقاومة التدحرج هي المؤثرة فقط)
تطبيق معادلات الحركة	m g = m a + AR a = g – (AR/m)	w sin θ – fr w cos θ = m a m g sin θ – fr m g cos θ = m a a = g (sin θ – fr cosθ)
- النتيجة في حالة اخذ المقاومات في الحسبان	العجلة تقل عند أخذ مقاومة الهواء في الحسبان, ولكنها تختلف من جسم لأخر حسب شكل الجسم (مقاومة الهواء AR و كتلة الجسم)	العجلة يكون لها مقدار أقل يعتمد على مقدار الميل ولا تعتمد العجلة على كتلة ووزن السيارة
تطبيق معادلة الطاقة	PE = KE + resistance work on body
	w h = ½ m v^2 + (AR) h m g h = ½ m v^2 + (AR) h v = √(h [g – (AR) /m])	w h = ½ m v^2 + (RR) L w h = ½ m v^2 + w cos θ fr L m g h = ½ m v^2 + m g cos θ fr L g L /sin θ = ½ v^2 + g fr L cos θ v = √ (g L ((2/sin θ) – fr cos θ))
- النتيجة في حالة أخذ المقاومات في الحسبان	السرعة للجسمين تختلف قليل حسب شكل الجسم (مقاومة الهواء AR) وكتلة الجسم (m)	السرعة واحدة للسيارة في الحالتين ولكنها في الواقع أقل قليلا من سرعة السيارة عند إهمال المقاومات
تطبيقات معادلات الحركة	v = vo + a t = 0 + a t t = v / a t = {√(h [g – (AR) /m])} / {g – (AR/m)}	v = vo + a t = 0 + a t t = v /a t = [√ (g L ((2/sin θ) – fr cos θ))] / [g (sin θ – fr cosθ)]
- النتيجة في حالة أخذ المقاومات في الحسبان	يختلف الزمن حسب شكل الجسم (الابعاد) المؤثر على مقاومة الهواء, وكذلك كتلة الجسم m	زمن الوصول واحد للسيارة في الحالتين ولكنها في الواقع أقل قليلا من سرعة السيارة عند إهمال المقاومات

النتيجة النهائية عند أخذ المقاومات (الحالة الفعالية):
- في حالة اخذ مقاومة التدحرج للعجلات في الحسبان وإهمال مقاومة الهواء (للسرعات البطيئة), أو تساوي مقاومة الهواء لنفس السيارة المحملة والغير محملة (حيث لا يختلف الشكل الخارجي) فإن معدل تعجيل سرعة السيارة في الحالتين واحد (حالة اختلاف الكتلة),

وعليه تكون سرعة السيارة وزمن وصولها واحد في الحالتين (السرعةv متساوية في الحالة A والحالة B وتكون أقل قليلا من حالة عدم أخذ مقاومة التدحرج في الحسبان).

        -  في حالة السقوط الحر لجسم وأخذ مقاومة الهواء في الحسبان: فإن العجلة ستختلف حسب كتلة الجسم وشكله (ويكون هناك اختلاف طفيف في السرعة, وزمن وصل الجسم للأرض, حسب معطيات المعادلة).