السرعة (6)
Velocity

السرعة
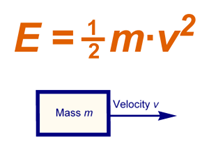
طاقة الحركة:	طاقة الحركة الانتقالية	طاقة الحركة الدورانية
الزخم	السقوط الحر لجسم	معامل الارتداد
التصادم ومدى الارتداد	نظم التصادم متعدد الابعاد	الدفعة
الأجزاء: 1 2 3 4 5 6

- طاقة الحركة Kinetic Energy (KE):

طاقة الحركة (المقصود بها هنا هي طاقة الحركة الانتقالية translational kinetic energy) وهي تعتمد على متغيرين هما كتلة الجسم mass (m), وسرعة الجسم speed (v). والمعادلة التالية تمثل طاقة الحركة لجسم:

KE = ½ mv²

طاقة الحركة هي كمية عددية scalar quantity؛ التي لها قيمة فقط مثل الشغل work, وطاقة الوضع potential energy, وليس لها اتجاه مثل السرعة velocity, والعجلة acceleration, والقوة force, الزخم momentum. وحدات طاقة الحركة (وطاقة الوضع, والشغل) بالنظام العالمي للوحدات هي الجول 1 Joule = 1 kg m²/s² = 1 N m, حيث كتلة الجسم m بالكيلوجرام, والسرعة v متر/ث, والقوة F نيوتن, والمسافة s بالمتر.

في الفيزياء كمية الحركة لجسم هي الطاقة التي يمتلكها الجسم نتيجة حركته. وتعرف بأنها الشغل اللازم لتعجيل/ تسارع الجسم ذو كتلة معينة من السكون حتى سرعته المحددة. مع اكتساب الجسم لهذه الطاقة خلال تسارعه, فإن الجسم يظل يحتفظ بهذه الطاقة إلا إذا تغيرت سرعته. وبالمثل يجب التأثير على الجسم بنفس كمية الشغل لتتباطأ سرعته حتى يصل إلى السكون.

التغيير في طاقة الحركة لجسم يساوي صافي الشغل المبذول على الجسم:

W_net= F d = ½ m v² – ½ m v_o² = ½ m (v² – v_o²)

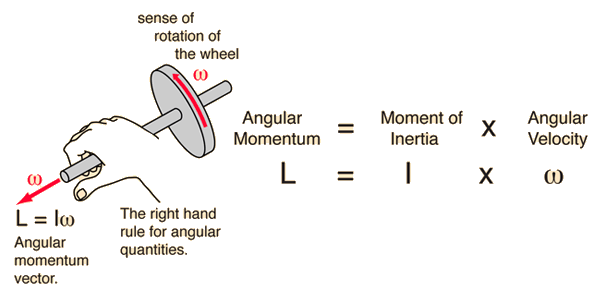
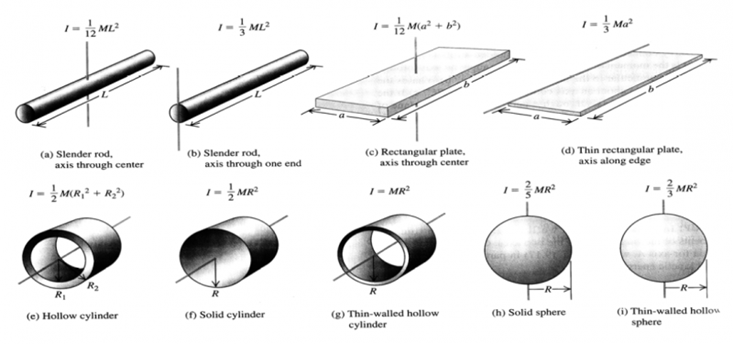
طاقة الحركة الدورانية Rotational kinetic energy:

KE_r = ∫ ½ v² dm = ∫ ½ (rω)² dm = ½ ω² ∫ r² dm = ½ I ω²

حيث:

ω السرعة الزاوية angular velocity

r المسافة بين مركز الثقل للجسم ومحور الدوران

I هي القصور الذاتي للجسم moment of inertia

File:Rot KE Mom Inertia 7.png

- الزخم Momentum (p):

الزخم الخطي linear momentum أو الزخم الانتقالي translational momentum هو مقدار الحركة التي بالجسم. هو حاصل ضرب الكتلة mass (m) في السرعة velocity (v) للجسم

p = mv

وحدات الزخم بالنظام العالمي للوحدات SI unit هي كيلوجرام متر/ ث kg m/s أو نيوتن ثانية N s. الزخم مثل السرعة هو كمية متجهة vector quantity, الذي له مقدار magnitude واتجاه direction, ويكون الزخم للجسم في نفس اتجاه سرعة الجسم. الزخم الخطي هو أيضا كمية محفوظة conserved quantity, أي في حالة النظام المغلق closed system فإنها لا تتغير ما لم تؤثر عليها قوة خارجية.

حالة سقوط جسم من السكون (السقوط الحر free falling) Object falling from rest:

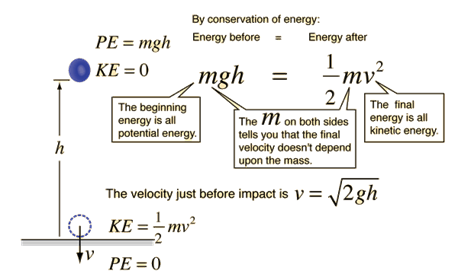
في حالة سقوط جسم من السكون تتحول طاقة الوضع (PE) gravitational potential energy إلى طاقة حركة kinetic energy (KE) في حالة اهمال مقاومة الهواء وتطبيق الحفاظ على الطاقة conservation of energy. حيث مجموع الطاقة عند بداية الحركة من على ارتفاع h تساوي مجموع الطاقة عند نهاية الحركة.

(PE + KE)_h = (PE + KE)₀

mgh + 0 = 0 + ½ m v²

وتكون سرعة الجسم بعد قطع مسافة h سقوطا من السكون هي

v = √2gh

- التصادم collisions:

قانون حفظ الزخم ليس كافي لوحده لتحديد حركة الجسم بعد التصادم. خاصية أخرى للحركة يجب معرفتها وهي طاقة الحركة. في حالة أن طاقة الحركة تكون محفوظه (لا يوجد فقد في طاقة الحركة), فأن التصادم يطلق عليه التصادم المرن elastic collision, وفي حالة عدم المحافظة على الطاقة يكون تصادم غير مرن inelastic collision. تعتمد حالة التصادم على قيمة معامل الارتداد.

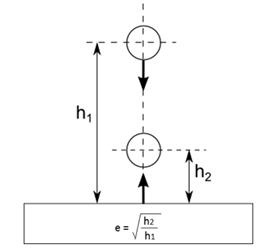
- معامل الارتداد Coefficient of restitution (COR):

يمكن التعبير عنه عن طريق المسافات (مسافة السقوط الحر drop height ومسافة الارتداد bounce height)

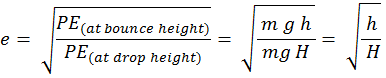
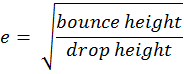
النسبة بين مسافة الارتداد إلى مسافة السقوط الحر h₂/h₁ (bouncing):

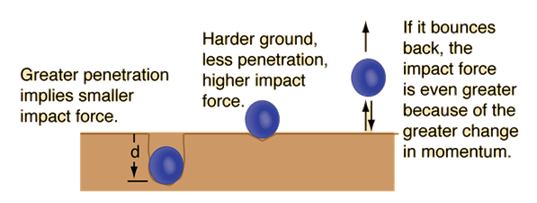
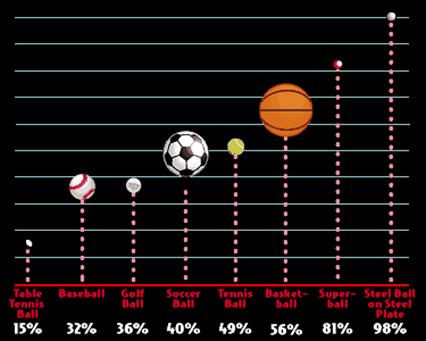
وهي احدى الطرق المتبعة للحكم على حالة النفخ للكرة المستخدمة في المباريات الرياضية. حيث يمكن الحكم على مقدار نفخ الكرة (ضغط الهواء) أو صلاحيتها عن طريق اسقاطها من ارتفاع معلوم على أرض صلبة وملاحظة ارتفاع الكرة المرتدة. يجب أخذ صلابة أرض الملعب في الاعتبار عند القيام بذلك. أو تستخدم الطريقة للمقارنة بين كرتين على نفس الأرضية, الكرة ذات النفخ الأكثر ترتد أعلى من الأخرى.

معامل الارتداد هو COR (e) كذلك مقارنة بين طاقة الحركة للجسم قبل الاصطدام مباشرة وبعد الاصطدام مباشرة:

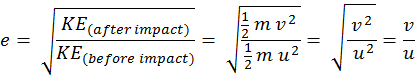
e = u/v

معامل الارتداد = السرعة النسبية بعد التصادم/ السرعة النسبية قبل التصادم,

Coefficient of restitution (e) = relative speed after collision/relative speed before collision

أي أن معامل الارتداد COR (e) يعرف أيضا بأنه النسبة بين السرعة النسبية قبل وبعد التصادم, في نفس اتجاه التصادم.

وعليه يمكن تعريف سرعة الارتداد بناء على معرفة سرعة الاقتراب ومعامل الارتداد وتكون:

سرعة التباعد = معامل الارتداد × سرعة الاقتراب

Speed of separation = e x speed of approach

- التصادم ومدى معامل الارتداد Range of values of e:

معامل الارتداد دائما رقم موجب ما بين صفر وواحد (0 and 1.0) [0 < e < 1]

e = 0, تعتبر هذه حالة تصادم غير مرن بالكامل perfectly inelastic collision:

الجسمين لا يبتعدان عن بعضهما بعد التصادم, ولكن يلتصقا ببعضهما البعض. طاقة الحركة تتحول إلى حرارة أو شغل في تشكيل الجسمين.

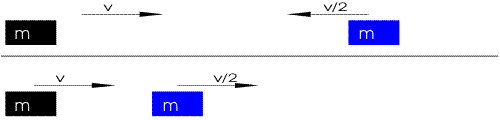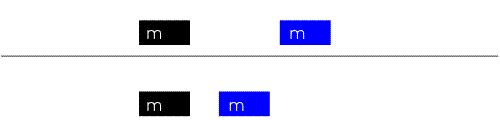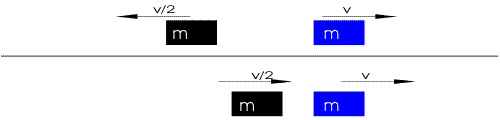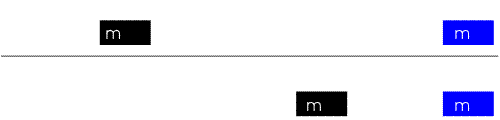
A perfectly inelastic collision between equal masses, one is stationary
Before collision:

u₁ = v, u₂ = 0

After collision:

From (Eq. 6) v₁ = v₂= ½ v

0 < e <1, هذه حالة التصادم الفعلية real-world inelastic collision:

والتي يكون فيها فقد لبعض من طاقة الحركة. في صورة شغل أو في صورة تحويل للطاقة.

e = 1, هذه حالة المرونة التامة perfectly elastic collision:

التي فيها لا يحدث فقد في طاقة الحركة, والجسمين يرتدا/ يبتعدا عن بعضهما بنفس السرعة النسبية التي اقتربا بهما من بعضهما البعض.

وهي الحالة التي يكون فيها الحفاظ على طاقة الحركة والحفاظ على الزخم بين الجسمين قبل وبعد التصادم.

في حالة التصادم بالمواجه المرن بين جسمين يمكن التعبير عنها في البعد الواحد, على طول الخط الواصل بين الجسمين. في حالة أن السرعات للجسمين m₁ و m₂ قبل التصادم هي u₁ و u₂ والسرعات v₁ و v₂بعد التصادم, فإن المعادلات التي تعبر عن الحفاظ عن الزخم وطاقة الحركة هي:

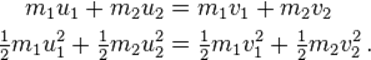
${\begin{aligned}m_{1}u_{1}+m_{2}u_{2}&=m_{1}v_{1}+m_{2}v_{2}\\{\tfrac {1}{2}}m_{1}u_{1}^{2}+{\tfrac {1}{2}}m_{2}u_{2}^{2}&={\tfrac {1}{2}}m_{1}v_{1}^{2}+{\tfrac {1}{2}}m_{2}v_{2}^{2}\,.\end{aligned}}$

Elastic collision of equal masses, one stationary

u₁ = v, u₂ = 0

Elastic collision of unequal masses, same speed

Before collision:

u₁ = v, u₂ = -v

After collision:

From (Eq. 3) v₁ = 0,

From (Eq. 4) v₂ = v

After collision:

From (Eq. 3) v₁ = - 1/3 v

From (Eq. 4) v₂ = + 5/3 v

السرعة بعد التصادم speed after impact:

الحالة العامة للتصادم بين جسمين كتلتهما m₁, m₂ ومعامل الارتداد بينهما COR (e)

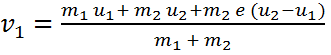…………….(1)

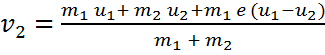…………….(2)

حيث
الجسم الأول:
كتلة الجسم m₁, السرعة قبل الاصطدام u₁, السرعة بعد الاصطدام v₁
الجسم الثاني:
كتلة الجسم m₂, السرعة قبل الاصطدام u₂, السرعة بعد الاصطدام v₂

* يجب اخذ اتجاه السرعة في المعادلة.

في حالة التصادم بين جسمين مرنين بالكامل تكون e= 1

بالتعويض بالمعادلتين السابقتين (1), (2) نصل إلى التالي

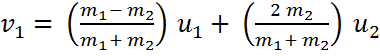……………(3)

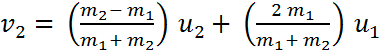…………….(4)

في حالة أن احد الجسمين له كتلة أكبر من الأخر, فإن سرعته ستتأثر قليلا بالتصادم في حين أن الجسم الاخر سوف تتعرض سرعته لتغيير كبير.


Elastic collision of equal masses different velocity (before collision):
u₁ = v, u₂ = ½ v	u₁ = v, u₂ = - ½ v
After collision:
Same direction From (Eq. 3) v₁ = 1/2 v From (Eq. 4) v₂ = v	Opposite direction From (Eq. 3) v₁ = - 1/2 v From (Eq. 4) v₂ = v

في حالة التصادم بين جسمين غير مرنين بالكامل تكون e = 0

بالتعويض في معادلة 1 أو 2 (في حالة حركة الجسمين) تكون المعادلة

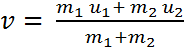…………..(5)

في حالة ان الجسم الثاني ساكن

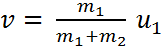………………(6)

يمكن الاستعانة ببرنامج اكسل التالي لحساب سرعة الارتداد للمعادلات من 1-6

www.thecartech.com/Autopedia/what/Collision2.xlsx

يلاحظ من البرنامج كذلك:
طاقة الحركة Kinetic energy KE:
في حالة التصادم المرن التام elastic collision؛ e = 1 يكون مجموع طاقة الحركة للجسمين بعد التصادم تساوي نفس مجموع طاقة الحركة للجسمين قبل التصادم (لا يوجد فقد).
في حالة التصادم الغير مرن التام inelastic collision؛ e = 0 يكون مجموع طاقة الحركة للجسمين بعد التصادم تقل كثيرا بعد التصادم من مجموع طاقة الحركة للجسمين قبل التصادم.
في حالة التصادم الغير مرن جزئيا partial inelastic collision؛ 0< e <1 يكون مجموع طاقة الحركة للجسمين بعد التصادم له قيمة بين حالة التصادم المرن التام والتصادم الغير مرن التام.
الزخم Momentum M:
في كل الحالات نجد ان الزخم متساوي (لا يوجد فقد), حيث لا يوجد احتكاك بين الاجسام المنزلقة والأرض.
* مع وجود احتكاك, فإن بعض الزخم من الاجسام سوف ينتقل إلى السطح الذي تنزلق عليه الأجسام. وبالمثل, في حالة وجود مقاومة هواء, فأن الزخم للجسمين سينتقل منه جزء إلى الهواء.

حالة التصادم الغير مرن جزئيا هي أكثر الاشكال شيوعا في العالم الحقيقي. في هذا النوع من التصادم, فالأجسام الداخلة في التصادم لا تلتصق مع بعضها البعض, ولكن بعض طاقة الحركة ما زالت تفقد. الاحتكاك, الصوت, الحرارة هي بعض الصور التي قد تفقد فيها طاقة الحركة خلال التصادم المرن الجزئي/ التصادم الغير مرن الجزئي.

e < 0, حالة اختراق penetration:

قيمة المعامل خارج المدى, في هذه الحالة يحدث اختراق لجسم صغير أكثر كثافة في جسم في اكبر, اقل كثافة مثل رصاصة تخترق لوحة التصويب.

- التصادم متعدد الابعاد Multiple dimensions collision:

التصادم في الحالات السابقة يمكن أن يطلق عليه التصادم في البعد الواحد (التصادم خلال الخط الواصل بين الجسمين).

المثال التالي يبين حالة تصادم ثنائي الابعاد, حيث لا توجد حركة متعامدة على مستوى الشكل, حيث هناك كميتين فقط لتمثيل السرعة والزخم. الخطين الازرقين يمثلا السرعات بعد التصادم, وعند إضافتهم اتجاهين نحصل على السرعة الابتدائية باللون الأحمر.

الحركة الفعلية لها مقدار واتجاه وتمثل السرعة v عن طريق متجهة. في الابعاد الثلاثة:

$\mathbf{v} = \left(v_x,v_y,v_z \right).$

وبالمثل الزخم:

$\mathbf{p} = \left(p_x,p_y,p_z \right).$

حيث يتم استبدال القيم للزخم والسرعة p, v بالمتجهات p, v (المتجهات تمثل بحروف بخط عريض). وتكون معادلة الزخم كالتالي:

p = m v

وتمثل معادلة المتجهة للزخم vector equation ثلاث معادلات عددية scalar equation

$\begin{align} p_x &= m v_x\\ p_y &= m v_y \\ p_z &= m v_z. \end{align}$

- الدفعة Impulse:

القوة المؤثرة لفترة زمنية على جسم سوف تؤدي إلى تغير زخم الجسم. في حالة تأثير القوة في اتجاه حركة الجسم فإنها تؤدي إلى زيادة سرعة وزخم الجسم, والعكس صحيح. الجسم (السيارة) الذي له زخم يمكن توقيفه عن طريق التأثير بقوة (الفرامل) لفترة من الوقت.

هذا المفهوم نابع من قانون نيوتن الثاني للحركة.

F = m a

F = m ∆v/∆t

F ∆t = m ∆v

في الفيزياء F t (القوة × الزمن) يعرف بالدفعة impulse. وحيث أن m v تعرف بالزخم, فتكون الكمية m ∆v تعرف بالتغيير في الزخم change in momentum. وعليه تصبح المعادلة:

Impulse = Change in momentum

وتعرف الوحدات للدفعة نيوتن ثانية (كجم متر/ث) (kg m/s) N s. وهي كمية متجه, في اتجاه القوة.

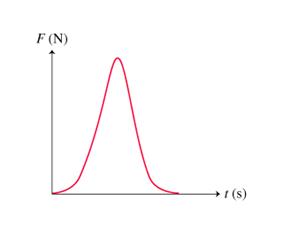
المساحة تحت منحنى القوة والزمن تمثل الزخم

https://en.wikipedia.org/wiki/Kinetic_energy
https://en.wikipedia.org/wiki/Momentum
https://en.wikipedia.org/wiki/Impulse_%28physics%29
https://en.wikipedia.org/wiki/Coefficient_of_restitution