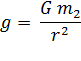السرعة (2)
Velocity

التغيير في السرعة
معدل تغيير السرعة (العجلة)	العجلة الثابتة	العجلة والقوة
عجلة الجاذبية الارضية	الكتلة والوزن	معدل تغيير العجلة
استخدام العجلة كبيان للقوة	سرعة السقوط الحر للأجسام	السرعة القصوى للسقوط الحر
الحركة الدائرية
الأجزاء: (1) 2 3 4

التغيير في السرعة
Change of Velocity

معدل تغيير السرعة a (العجلة) & deceleration acceleration:

العجلة a هي معدل تغيير السرعة بالنسبة للزمن a = dv/dt. في حالة تزايد سرعة الجسم تسمى تسارع أو عجلة تزايديه  accelerationوتأخذ إشارة موجبة, في حالة تباطئ سرعة الجسم تسمى تباطئ أو عجلة تقصييريه deceleration وتأخذ إشارة سالبة. وحدة العجلة متر/ثانية تربيع (m/s²). تغيير سرعة الجسم (حدوث عجلة) تأتي نتيجة تأثير قوة خارجية كما تبين قوانين نيوتن للحركة:

1- القانون الأول: جميع الأجسام تظل على حالتها من السكون أو الحركة بسرعة ثابتة في خط مستقيم مالم تؤثر عليها قوة خارجية.

2- القانون الثاني: التغيير في السرعة (العجلة a) تتناسب طرديا مع القوة المؤثرة على الجسم F, في أتجاه محصلة القوة, وتتناسب عكسيا مع كتلة الجسم m, فتكون معادلة الحركة F = ma.

3- القانون الثالث: عند تلامس جسمين فإن القوة المؤثرة بين الجسمين, الفعل ورد الفعل يكونا متساويين في المقدار ومتضادان في الاتجاه. لكل فعل رد فعل مساوي له في المقدار ومضاد له في الاتجاه.

المعادلات التي تربط المسافة مع السرعة مع الزمن, والتي تحتوي على المتغيرات التالية suvat  يطلق عليها suvat equations (suvat هي المتغيرات بالمعادلة). العجلة تكون ثابتة uniform or constant acceleration أي لا تتغير قيمتها مع الزمن:

v = u + a t

s = u t + ½ a t²

v² = u² + 2 a s

حيث:
v = السرعة النهائية (m/s)
u = السرعة الابتدائية (m/s)
s = المسافة المقطوعة (m)
a = عجلة الجسم (m/s²)
t = الزمن (s)

العجلة الثابتة constant (uniform) acceleration :

العجلة الثابتة هي نوع من أنواع الحركة والتي تكون سرعة الجسم تتغير بمقدار ثابت على فترات زمنية متساوية.

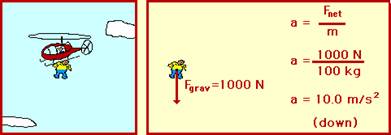
العجلة والقوة acceleration and force:

عند تأثير قوة على جسم فإنها تكسبه عجلة بناء على المعادلة التالية:

a = F/m

وتعرف المعادلة على إنها قانون نيوتن الثاني للحركة

F = m a

وتكون وحدة القوة تقاس كجم متر/ث² kg m/s²

حيث أن وحدة القوة بالوحدات العالمية نيوتن N هي

1 N = 1 kg m/s²

عجلة الجاذبية الأرضية g gravitational acceleration:

هي عجلة الجسم الناجمة عن قوة جذب الأرض. مع إهمال مقاومة الهواء فإن تسارع الأجسام في مجال جاذبية الأرض يكون لها نفس المعدل حسب بعدها عن مركز الأرض.

قانون الجاذبية بين الأجسام المختلفة تساوي

حيث:
G = ثابت الجاذبية = s² 6.67384 x 10^-11 m³/kg
m₂ = كتلة جسم 2 (كتلة الأرض) = 5.97219 × 10²⁴ kg
r = بعد الجسم عن مركز جسم 2 (الأرض) = المسافة بين سطح الأرض ومركز الأرض = 6378100 m

فتكون قيمة عجلة الجاذبية الارضية تساوي:

* العجلة الناجمة عن الجاذبية الأرضية لا تعمد على كتلة الجسم. وتتراوح قيمة الجاذبية الأرضية ما بين  9.78- 9.82 m/s² حسب خطوط العرض, والقيمة القياسية  gهي  9.80665 m/s² وتقرب إلى 9.81 m/s². الأجسام ذات الكثافة القليلة (الريشة) تتسارع بمقدار أقل نتيجة مقاومة الهواء لها.

مثال على عجلة الجاذبية للأجرام السماوية المختلفة:

الجسم	نسبة من عجلة الجاذبية الأرضية	مقدار العجلة m/s^2
الشمس	27.0 g	274.1
كوكب الزهرة	0.9032 g	8.872
كوكب الأرض	1g	9.806 ~ 9.81
كوكب المريخ	0.3895 g	3.728
القمر	0.1655 ~ 1/6 g	1.625

الكتلةm  والوزنw mass & weight :
وزن الجسم هو قوة جذب الأرض لكتلة الجسم.

F = m a

w = m g

* وحدة الكتلة (kg), وحدة الوزن (N), وعجلة التسارع (a = g).

ويكون وزن 1 كتلة 1 كجم تساوي w = 9.81 N

* الفرق بين الكتلة والوزن: الكتلة هي مقدار المادة التي يحتويها الجسم, والوزن هو قوة جذب الأرض لكتلة الجسم.

معدل تغيير العجلة rate of change of acceleration:

معدل تغيير العجلة هي تفاضل العجلة بالنسبة للزمن أو التفاضل الثاني للسرعة بالنسبة للزمن, أو التفاضل الثالث للإزاحة بالنسبة للزمن, ويطلق عليه العديد من المسميات كالهزة أو الرجفة  jerk, jolt, surge, or lurch. ويرمز له بالرمز j.

حيث:
 = معدل تغيير العجلة (m/s³)
 = العجلة (m/s²)
 = السرعة  (m/s)
 = الإزاحة    (m)
t = الزمن (s)

استخدام العجلة كبيان للقوة (F = ? g) g-force (acceleration):

يتم التعبير عن القوة بقيمة العجلة التي يتعرض لها الجسم كنسبة من عجلة الجاذبية الارضية (السقوط الحر) في العديد من التطبيقات, وخاصة التي لها علاقة بالكتلة, كالصعود في صاروخ أو الوقوف على مستوى مائل أو السير في منحنى دائري. حيث تختلف قيمة القوة باختلاف الكتلة.

مثال على هذا:

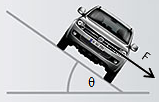
عند وقوف السيارة على مستوى مائل فإن السيارة تتعرض لقوة جانبية مقدارها

F = w sin θ = (m g) sin θ
F = m a = m g sin θ
a = g sin θ = (sin θ) g

عند وقوف السيارة على طريق مائل بزاوية 30 درجة فإنها تتعرض لقوة مقدراها
F = (sin 30) g = - 0.5 g. هذا يدل على مقدار القوة التي تتعرض لها السيارة بالنسبة لميل المنحنى ولا يتكلم عن قيمة القوة المطلقة, هذا هو ما سوف تتعرض له السيارة بغض النظر عن كتلتها, أي سيارة سوف تقف على هذا المنحنى سوف تتعرض لقوة مقدراها 0.5 g, ويكون مقدار القوة الفعلي يساوي هذا الرقم مضروب في كتلة السيارة. القوة بمقياس عجلة الجاذبية g, تأتي من رد الفعل (قوة ميكانيكية) أي لاتزان السيارة على المنحني في المثال السابق تحتاج إلي قوة بين الإطارات والسيارة من الارض تساوي 0.5 g بإشارة موجبة.

وحدة القوة g ليس واحدة من الوحدات العالمية SI unit حيث “g” تعني جرام ولا يجب الخلط بينها وبين “G” الذي يعتبر ثابت الجاذبية.

مثال	قوة عجلة الجاذبية (g-force)
الوقوف على الكرة الأرضية عند خط الاستواء	1g
القوة على السائق لسيارة Bugatti Veyron تتسارع من صفر إلى 100 كم/ساعة خلال 2.4 ثانية	1.55 g
مكوك الفضاء خلال الانطلاق والعودة	3 g
سيارة فورميلا 1  إثناء فرملة قوية	+5 g
سيارة فورميلا 1  أقصى قوة مركزية عند الدوران في منحنى	5-6 g
الوفاة في حادث أو إصابات بليغة	> 25 g

* تحمل الإنسان لتأثير القوة يعتمد على مقدار قوة القوة g-force, مدة التعرض, اتجاه القوة, مكان التأثير, وضعية الجسم. يظهر تأثير تلك القوة على طياري الطائرات المقاتلة.

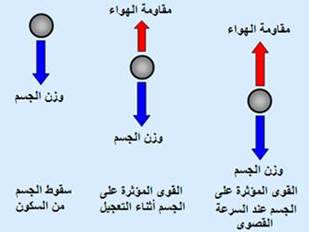
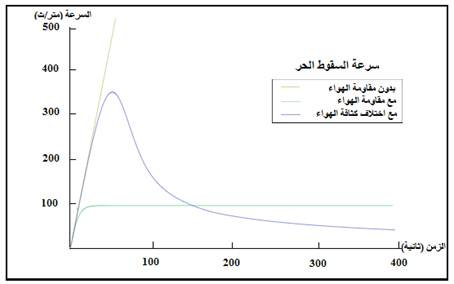
سرعة السقوط الحر للأجسامspeed of falling bodies :

 سرعة سقوط الأجسام (مع عدم الأخذ بمقاومة الهواء والاحتكاك) لنفس مسافة السقوط تكون متساوية على الرغم من اختلاف كتل تلك الأجسام.

من المعادلة v² = u² + 2 a s بالتعويض عن السرعة الابتدائية u = 0  والعجلة  a = gفتكون سرعة السقوط عند أي مسافة سقوط s تساوي

ولا تؤثر كتلة الجسم على سرعة سقوطه كما يظهر من المعادلة عدم وجود ذكر للكتلة. وعليه يكون زمن السقوط متساوي لجميع الأجسام (عند إهمال مقاومة الهواء والاحتكاك).

* في أواخر 1500, كان الناس تعتقد أن الجسم الأثقل يهبط أسرع من الجسم الأخف وزنا. كما كان معروف من أيام أرسطو. ويعزى إلى جاليلو جاليلي الذي كان يشغل منصب استاذ رياضيات في جامعة بيزا بضحط هذا الاعتقاد, حيث يقال أنه قام بأسقاط جسمين مختلفين الوزن (الكتلة) من برج بيزا المائل حيث برهن على سقوطهما في نفس الزمن. كان تحديه لمعتقدات أرسطو أن فقد منصبه بالجامعة جراء ذلك.

السرعة القصوى للسقوط  (الهبوط)  terminal velocity (v_terminal):

هي السرعة القصوى التي يصل إليها الجسم أثناء سقوطه. مع أخذ مقاومة الهواء في الاعتبار تزداد مقاومة الهواء مع مربع سرعة الجسم أثناء سقوطه, حتى تصير القوة الخارجية المؤثرة على الجسم تساوي صفر (مقاومة الهواء تساوي وزن الجسم), وعندها تصبح عجلة الجسم تساوي صفر أي أن سرعة الجسم تبق ثابتة, وتسمى السرعة القصوى لسقوط الجسم. تعتمد قيمة السرعة القصوى على وزن الجسم (كتلته) ومعامل مقاومة الهواء الذي يعتمد على شكل انسيابية الجسم, ومساحة مقطع الجسم المواجه للهواء, وكثافة الهواء أو المائع الذي يسقط به الجسم.

عند السرعة القصوى تتساوى مقاومة الهواء مع وزن الجسم كما في المعادلة:

وتكون السرعة القصوى للسقوط تساوي:

حيث:
v_terminal = السرعة القصوى (m/s)
m = كتلة الجسم  (kg)
g  = عجلة الجاذبية الأرضية (m/s²)
C  = معامل مقاومة الهواء
A = مساحة مسقط الجسم (m²)
ρ = كثافة الهواء (kg/m³)

السرعة القصوى لأجسام ساقطة, معامل مقاومة الهواء (ρ) = 0.5
الجسم الساقط	الكتلة	مساحة المقطع	السرعة القصوى
القفز من الطائرة (بدون مظلة)	75 كجم	0.7 م^2	60 م/ث	216 كم/س
كرة الجولف (نصف القطر 2.1 سم)	46 جم	14 سم^2	32 م/ث	115.2 كم/س
قطرة الندى (نصف القطر 0.2 سم)	0.034 جم	0.13 سم^2	9 م/ث	32.4 كم/س

* أول إنسان يتعدى سرعة الصوت خلال السقوط الحر:

قام الاسترالي فليكس بومجيرتنير Flex Baumgertner في 14 أكتوبر 2012 بالقفز من ارتفاع 39000 متر(39 كيلو متر) فوق روزويل نيومكسيكو. من بالون منفوخ بالهليوم, مرتديا بدلة فضاء. حيث وصل إلى سرعة 1342 (1.24 ماخ). وكانت درجة الحرارة عند ارتفاع القفز (- 57 درجة مئوية), والضغط الجوي 3.3 مللي بار (مساوي 0.33% من الضغط عند مستوى سطح الأرض). كثافة الهواء قيمتها ضئيلة جدا (قيمة متغيرة مع الارتفاع). وكان طول مسافة القفزة 6.76 كم.
*حقق عدة أرقام قياسية عالمية في (أعلى ارتفاع لمنطاد 39000 متر, أطول مسافة قفزة 6.76 كم, أسرع سقوط حر 1.24 ماخ).

وحيث أن السرعة القصوى تعتمد على تساوي مقاومة الهواء مع وزن الجسم, ولكن نظرا للارتفاع العالي وعدم ثبات القيم تصبح معادلة السقوط الحر

وعند حل المعادة بالطريقة العددية يمكن الحصول على سرعة السقوط الحر, والتي وصلت سرعة الجسم خلال مسافة السقوط إلى تعدي سرعة الصوت.

http://blog.wolfram.com/2012/10/24/falling-faster-than-the-speed-of-sound/

http://disipio.wordpress.com/2012/10/21/the-felix-baumgartner-equation/

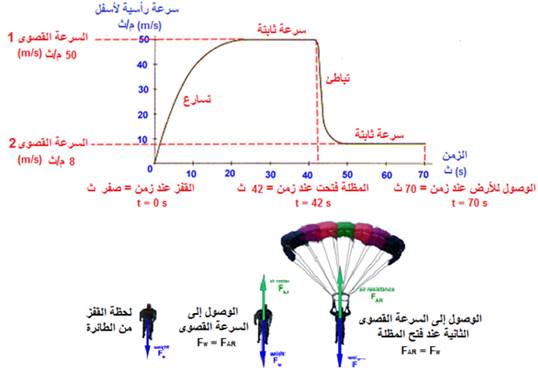
القفز بالمظلة:

عند القفز بالمظلة تكون سرعة الجسم في البداية تساوي صفر, تبدأ بعدها سرعة الجسم بالزيادة (تتكون عجلة للجسم نتيجة أن الوزن أكبر من مقاومة الهواء). تظل السرعة في تزايد حتى تكون مقاومة الهواء (التي تتناسب مع مربع السرعة) تساوي وزن الجسم وعندها تصل سرعة الجسم (السرعة القصوى 1), ويستمر السقوط بتلك السرعة. عند فتح المظلة تزيد مقاومة الهواء عن وزن الجسم فتتكون عجلة تقصيرية تقلل من سرعة الجسم, تقل سرعة الجسم حتى تصل إلى (السرعة القصوى 2), عندها تكون مقاومة الهواء (عالية نتيجة فتح المظلة) مساوية لوزن الجسم. تظل سرعة هبوط الجسم ثابتة حتى يصل الجسم إلى الأرض.

مثال عددي يبين بدأ الحركة من السكون  (فرق الوزن ومقاومة الهواء) يؤدي إلى تعجيل لسرعة الجسم حتى الوصول إلى السرعة القصوى للسقوط الحر. ثم فتح المظلة وزيادة مقاومة الهواء تؤدي إلى تباطئ  لسرعة الجسم حتي الوصول إلى السرعة القصوى مع مقاومة الهواء للمظلة. يظل السقوط بتلك السرعة حتى الوصول إلى الأرض.

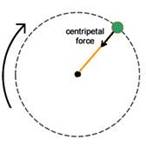
الحركة الدائرية circular motion:

تسمى السرعة للجسم بالسرعة الزاوية ω angular velocity, وهي معدل قطع الزوايا بالنسبة للزمن.  وقد تكون تلك السرعة ثابتة أو متغيرة, التغيير في السرعة الزاوية يساوي العجلة الزاوية. كما تتكون عجلة للجسم تتجه ناحية المركز.

- العجلة الزاوية αangular acceleration :

هي مقدار التغيير في السرعة الزاوية ω بالنسبة للزمن t. أي ان هناك تغيير في السرعة الزاوية بالنسبة للزمن.
α = dω/d

- العجلة في اتجاه القطر (a_c) radial or centripetal acceleration, هذه العجلة للجسم عندما يدور في مسار دائري وتتجه ناحية المركز. ويكون لها القيمة

a_c = v²/r = ω² r                   

القوة المؤثرة على جسم يدور بسرعة دائرية ثابتة, تتجه أيضا إلى مركز الدائرة, وتعرف القوة بقوة الجاذبية centripetal وهي القوة التي تحافظ على دوران الجسم بسرعة ثابتة في مدار دائري. ومن أمثلتها دوران جسم مربوط في حبل ويدور في دائرة, دوران القمر حول الأرض, دوران السيارة في طريق دائري, ....
عند إدارة كتلة مربوطة بحبل حول مركز دوارن, تعمل قوة الجاذبية على جذب الكتلة للداخل وتحافظ على جعلها تسير في مدار دائري, تلك القوة تساوي:

F = m a_c = m (v²/r) = mω²r

وتسمى القوة المؤثرة على الحبل وتشده للخارج بقوة الطرد المركزية centrifugal force, وهي فعل ورد فعل تتساوى القوتين في المقدار وتضاد في الاتجاه.