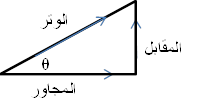
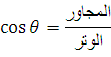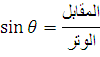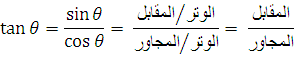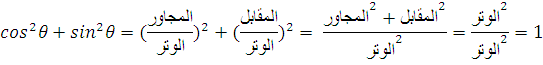المتجهات ومركباتها (طريقة التحليل)

Vectors and their components

$Description: Description: C:\Users\Kassem\Documents\My Site\subjects\Physics\Homework_44_files\image001.png$
$Description: Description: C:\Users\Kassem\Documents\My Site\subjects\Physics\Homework_44_files\image002.png$	$Description: Description: C:\Users\Kassem\Documents\My Site\subjects\Physics\Homework_44_files\image003.png$	$Description: Description: C:\Users\Kassem\Documents\My Site\subjects\Physics\Homework_44_files\image004.png$
$Description: Description: C:\Users\Kassem\Documents\My Site\subjects\Physics\Homework_44_files\image005.png$	$Description: Description: C:\Users\Kassem\Documents\My Site\subjects\Physics\Homework_44_files\image006.png$

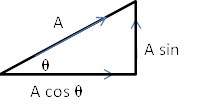
$Description: Description: C:\Users\Kassem\Documents\My Site\subjects\Physics\Homework_44_files\image007.png$

A = A cos θ i + A sin θ j

A² = (A cos θ)² + (A sin θ)²

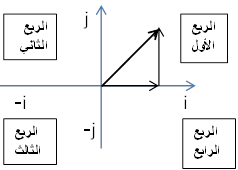
$Description: Description: C:\Users\Kassem\Documents\My Site\subjects\Physics\Homework_44_files\image008.png$ الربع الأول:

قيمة موجبة cos θ, sin θ, tan θ =
الربع الثاني:

قيمة موجبة sin θ =, قيمة سالبةcos θ, tan θ =
الربع الثالث:

قيمة موجبة tan θ =, قيمة سالبة cos θ, sin θ =

الربع الرابع:

قيمة موجبة cos θ =, قيمة سالبة sin θ, tan θ =

مثال:

أوجد المحصلة C لمجموع المتجه A والمتجه B, حيث A = 38 km, α = 60^o , B = 15 km, β = 120^o

الحل:

A = 38 cos 60 i + 38 sin 60 j, B = 15 cos 120 i + 15 sin 120 j

A = 19 i + 32.91 j, B = - 7.5 i + 12.99 j

C = A + B,

C = (19 – 7.5) i + (32.91 +12.99) j

C = 11.5 i + 45.9 j

حيث أن مركبة المحصلة في الاتجاه السيني موجبة, مركبة المحصلة في الاتجاه الصادي موجبة, إذا المحصلة C تقع في الربع الأول.

$Description: Description: C:\Users\Kassem\Documents\My Site\subjects\Physics\Homework_44_files\image009.png$

$Description: Description: C:\Users\Kassem\Documents\My Site\subjects\Physics\Homework_44_files\image010.png$

المحصلة C هي [ بالربع الأول [C = 47.32 km, γ = 75.93^o

واجب 4:

أوجد مجموع المتجهات التالية باستخدام محصلة مركبات المتجهات:

1- A = 20 N تصنع زاوية 30^o مع المحور السيني,
B = 40 N تصنع زاوية 60^oمع المحور السيني.

A = (20 cos 30) i + (20 sin 30) j
A = ………… i + ………….....j
B = (40 cos 60) i + (40 sin 60) j
B = ……….…. i + ……...…... j
C = A + B = ……….…. i + ……...…... j
$Description: Description: C:\Users\Kassem\Documents\My Site\subjects\Physics\Homework_44_files\image011.png$

$Description: Description: C:\Users\Kassem\Documents\My Site\subjects\Physics\Homework_44_files\image012.png$ بالربع الأول

2- A =60 N تصنع زاوية 40^o مع المحور السيني,
B = 40 N تصنع زاوية 120^oمع المحور السيني.

تمارين 4:

3- A =12 kN تصنع زاوية 145^o مع المحور السيني,
B = 15 kN تصنع زاوية 245^oمع المحور السيني.

4- A =20 cm تصنع زاوية 230^o مع المحور السيني,
B = 10 cm تصنع زاوية 300^oمع المحور السيني.

5- A =10 m تصنع زاوية 0^o مع المحور السيني,
B = 18 m تصنع زاوية 60^oمع المحور السيني.