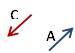الكميات المتجهة

Vector Quantities

- الكميات الفيزيائية

o الكميات القياسية

o الكميات المتجه

§ تمثيل المتجه

· الطريقة البيانية

· طريقة الإحداثيات (الكرتيزية)

§ تساوي وتضاد ومضاعفات وأجزاء المتجه

§ عمليات المتجهات

· تحليل المتجهات

· جمع المتجهات

· طرح المتجهات

· ضرب المتجهات

o الضرب القياسي

o الضرب الإتجاهي

§ المتجه بين نقطتين

§ متجه الوحدة

- برامج حسابية

- مواقع ذات علاقة

الكميات الفيزيائية Physical quantities:

هي خاصية فيزيائية, أو ظاهرة يمكن تقيمها عن طريق القياس (الإزاحة, الكتلة, الزمن, درجة الحرارة, السرعة,.....). ويمكن تقسيم الكميات الفيزيائية إلى كميات قياسية وكميات متجهة. ويرمز للكمية الفيزيائية بحرف, هذا الحرف اختياري ليس هناك قاعدة لاختيار الرمز ولكن العديد من تلك الرموز يتم اختياره حسب اتفاق المستخدمين وليس ملزما (الإزاحة: L, ل, x, H). وقد يضاف إلى الرمز حرف أو رقم لبيان المركبة أو العدد L₁, a_x, a_y, a_z), ل₁, .......). رموز الكميات القياسية التي تكتب بالمعادلة تختلف عن الوحدات المستخدمة لقياس تلك الوحدات, حيث أن الوحدات يجب أن تكتب بشكل موحد متفق عليه حسب نوع الوحدات المستخدم (الوحدات العالمية, الوحدة الأمبريالية) ولا يمكن الحياد عنه.

الكميات القياسية scalar quantities:

 يعبر عنها بمقدار فقط, رقم يبين المقدار (درجة الحرارة, الكتلة, الشغل ....), ويمكن إضافة إشارة إلى المقدار كدرجة الحرارة سالبة أو موجبة (د = -15 درجة مئوية).

الكميات المتجهة vector quantities:

أما الكمية المتجهة فيعبر عنها بمقدار واتجاه (الإزاحة, القوة, العزم ....), مقدار المتجه يعبر عنه كما يعبر عن الكمية القياسية ويضاف عليه اتجاه تلك الكمية (الإزاحة = 10 م في الاتجاه الموجب للمحور السيني).

التعبير عن الكميات القياسية والمتجهة:

يعبر عن الكميات القياسية والمتجه في المعادلات برمز يرمز لتلك الكمية, للتفريق بين رمز الكمية المتجهة ورمز الكمية القياسية. ويكتب رمز الكمية المتجهة بحرف يكتب كالتالي:  m, m, , ويرمز للكمية القياسية بحرف يكتب بالطريقة العادية m. ويعبر عن قيمة المتجهة برمز المتجه داخل علامة القيمة المطلقة كالتالي m = |m|. 

تمثيل المتجهة vector representation :

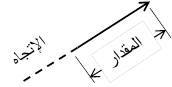
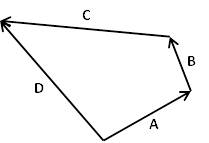
* الطريقة البيانية: يمثل المتجهة بالرسم عن طريق سهم,

حيث يمثل طول السهم المقدار (كطول أو يمثل بمقياس رسم), وتمثل الزاوية التي يصنعها السهم اتجاه المتجهة, ويشير رأس السهم إلى اتجاه مسار المتجهة.

* طريقة المركبات: يمكن التعبير عن المتجه B عن طريق متجهات تمثل مركبات المتجه, مركبة المتجه في كل من الاتجاه السيني (س (x والاتجاه الصادي (ص (Y والاتجاه العايني (ع (z.

B = B_x + B_y +B_z

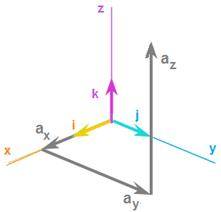
*  طريقة الأحداثيات: صيغة الاحداثيات الكرتيزية: يمكن تمثيل المعادلة السابقة المتجه الأصلي B يساوي مجموع 3 متجهات B_x, B_y, B_z كل متجه يمثل مقدار مركبة المتجه الأصلي  واتجاهها في إتجاه أحدى المحاور.

B = B_x i + B_y j +B_z k

# يمثل كل من المتجهات الثلاثة بمقدار B_x, B_y, B_z واتجاه i, j, k, يمثل المقدار بمقدار (مركبة المتجه الأصلي بالنسبة للمحور), ويمثل الاتجاه بمقدار متجه الوحدة (متجه اتجاهه في الاتجاه الموجب لأحد المحاور الرئيسية ومقداره يساوي واحد).

مثال: B = 5 i + 2 j - 3 k

* الأشارة السابقة لكل مركبة للمتجه تعطي اتجاه تلك المركبة على المحور الخاص بها, أي أن الأشارة الموجبة "+" تعني أن متجه المركبة يتجه في الاتجاه الموجب للمحور, والإشارة السالبة "-" تعني أن متجه المركبة يتجه في عكس الاتجاه الموجب للمحور (الاتجاه السالب).

حيث أن:

B_x = مقدار مركبة المتجه في الاتجاه السيني س (x)  = B cos α
B_y = مقدار مركبة المتجه في الاتجاه الصادي ص (Y) = B cos β
B_z = مقدار مركبة المتجه في الاتجاه العيني ع (Z) = B cos γ

حيث: α, β, γ الزوايا التي يصنعها المتجه B مع المحور السيني x والصادي y والعيني z بالترتيب.

i = متجه الوحدة في الاتجاه السيني x, مقدار المتجه يساوي 1

j = متجه الوحدة في الاتجاه الصادي y, مقدار المتجه يساوي 1

k = متجه الوحدة في الاتجاه العيني z, مقدار المتجه يساوي 1

* حيث أن متجه الوحدة هو متجه مقداره (1), فبضرب متجه الوحدة في مقدار قيمة المركبة يعطي متجهه له مقدار (نفس المقدار العددي) واتجاه (اتجاه المحورحسب رمز المتجه). أي أن (B_x i) تمثل متجه مقداره B_x ويتجه في الاتجاه الموجب للمحور السيني x.

* يمكن الحصول على مقدار قيمة مقدار المتجه  Bوالتي تساوي B من المعادلة التالية:

المتجهات ثنائية الأبعاد

2-Dimensions vectors

  المتجه ثنائي الأبعاد هو متجه يتواجد في بعدين فقط, مثل المتجه المرسوم على سطح الصفحة. أي له مركبتين فقط, واحدة في الاتجاه السيني (x) والأخرى في الاتجاه الصادي (y), والمركبة في الاتجاه العيني (z) المتعامد على الصفحة تساوي صفر.

تمثيل المتجه:

- صيغة الأبعاد الكرتيزية:

يمكن التعبير عن المتجه بمركباته في الاتجاه السيني والصادي. بحيث يمثل الرقم العددي في الجهة اليمنى بالمعادلة مقدار مركبة المتجه, ويمثل الحرف التابع للرقم اتجاه المركبة ( i يعبر عن متجه الوحدة في الاتجاه السيني, j يعبر عن متجه الوحدة في الاتجاه الصادي)

مثال: C = 3 i + 4 j

- الصيغة المركزية Polar form:

يمكن التعبير عن المتجهة A كمقدار واتجاه, حيث يمثل الرمز A المقدار وتمثل الزاوية α التي يصنعها المتجهة مع المحور السيني الموجب الاتجاه, )α = A at (A.

- التمثيل البياني للمتجه:

يمثل المتجه بسهم, يكون طول المتجه يمثل مقدار المتجه (ويرسم بمقياس رسم: تمثل وحدة المسافات مقدار معين من الطول الحقيقي للمتجه), واتجاه السهم هو اتجاه المتجه.

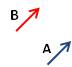
تساوي وتضاد ومضاعفة وأجزاء المتجه:

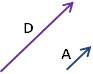
تساوي	تساوي وتضاد	مضاعفات	أجزاء	تضاد ومضاعفات
B = A	C = - A	D = 3 A	E = 0.5 A	F = - 2 A

عمليات المتجهات

Vector operations

تحليل المتجهات  Resolving vector into components :

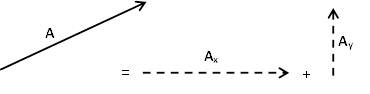
المقصود بتحليل المتجه هو إيجاد مركبة المتجه في الاتجاه السيني (متجه سيني), ومركبة المتجه في الاتجاه الصادي (متجه صادي), بحيث يكون المجموع الاتجاهي للمتجهين يعطي المتجه الأصلي.

A = A_x + A_y

كما يمكن كتابته بالصورة التالية (الأبعاد الكرتيزية)                      

A = A_x i + A_y j

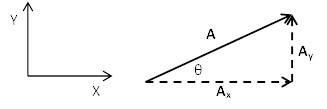
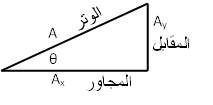
ويكون مقدار المتجه A هو القيمة A, ويكون مقدار المتجهة A_x هو القيمة  A_x, ويكون مقدار المتجهة A_y هو القيمة  A_y. يرسم مقدار المتجهات (المتجه الأصلي, ومتجهي المركبتين)  في مثلث كما في الشكل

بالمثلث تمثل أبعاد أطوال أضلاع المثلث مقدار قيمة كل متجه. الدوال المثلثية بالمثلث تكون كالتالي:

- جا هـ (sin θ)  = المقابل/ الوتر = A_y مقسومة على A,

 أي أن sin θ=A_y / A , ومنها A_y = A sin θ

- جتا هـ (cos θ)  = المجاور/ الوتر = A_x ,مقسومة على  A,

أي أن cos θ=A_x / A , ومنها A_x = A cos θ

- ظا هـ (tan θ)  = المقابل/ الوتر = A_y  مقسومة على A_x, أي أن tan θ=A_y / A_x , ومنها

θ = tan^-1 θ =tan ^-1( A_y /A_x)

- وحسب نظرية فيثاغورث للمثلث قائم الزاوية         

مثال أ:

أوجد الصيغة الأبعاد الكرتيزية للمتجهة  A

A = A cos α i + A sin α j = 20 cos 60 i  + 20 sin 60 j = 10 i + 17.32 j

مثال ب:

أوجد مقدار متجه المسافة (m) B واتجاهه, B = 5 i – 12 j

جمع المتجهات  Vectors addition:

يمكن جمع المتجهات بطريقة الرسم أو بطريقة جمع مركبات المتجهات. . ترتيب جمع المتجات لا يؤثر على نتيجة الجمع, فإن c = a + b = b +a . طرح المتجهات هي نفس عمليات الجمع للمتجهات ولكن مع تغيير إتجاه المتجه للجهة الأخر عند استخدام الأسهم لتمثيل المتجه, وعكس إشارة المتجه المطروح في حالة استخدام الجمع الجبري.

طرق جمع المتجهات:

1- الجمع الجبري للمتجهات:
تجمع المتجهات جمع جبري فقط  (في حالة أن المتجهات لها نفس الاتجاه) مع الأخذ في الاعتبار اتجاه السهم.

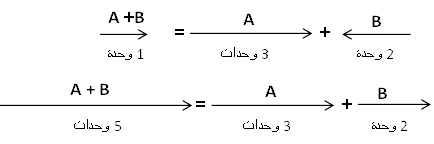
مثال:

شخص سار مسافة 100 متر في اتجاه الشمال ثم سار 200 متر في اتجاه الجنوب, كم يبعد هذا الشخص عن نقطة البداية؟

الحل:

100 - 200 = 100 متر في اتجاه الجنوب

2- الجمع والطرح البياني للمتجهات:

في حالة أن المتجهات ليس لها نفس الاتجاه يكون الجمع بأحدى الطرق التالية.

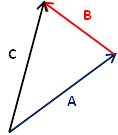
أ- طريقة التوالي (متعدد الأضلاع) head-to-tail (polygon) method:

C = A + B

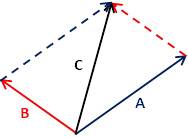
ب-  طريقة متوازي الإضلاع parallelograms method:
C = A + B

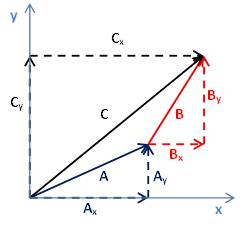
طريقة جمع مركبات المتجهة method of components:

تحلل المتجهات إلى المركبة السينية والصادية, تم تجمع جمع جبري المتجهات في الاتجاه السيني وكذلك المتجهات في الاتجاه الصادي, حيث المركبات في الاتجاه السيني لها نفس الاتجاه والمركبات في الاتجاه الصادي لها نفس الاتجاه.

C = A + B                           
= (A_x + A_y) + (B_x + B_y)   
 = (A_x +B_x) +(A_y+ B_y)     
 = (A_x +B_x) i + (A_y +B_y) j
= C_x i + C_y j                   

ويكون مقدار المحصلة (المتجه C) يساوي:

وتكون الزاوية التي تصنعها المحصلة (المتجه C) تساوي:

ويراعي إشارات C_x , C_y حسب الشكل التالي:

مثال: أوجد مجموع المتجهين:

أ- تحويل كلا المتجهين إلى مركباتهم في الاتجاه السيني والصادي

A = Ax + Ay A = A cos α i + A sin α j A  = 10 cos 60 i + 10 sin 60 j A  = 5 i + 8.66 j

B = Bx + By B = B cos β i + B sin β j B  = 5 cos 330 i + 5 sin 330 j B  = 4.33 i – 2.5 j

ب- نجمع جمع جبري لمركبة المتجهين لكلا المركبة السينية والمركبة الصادية

C = A + B                                      

C = (A_x + A_y) + (B_x + B_y)          

C = (A_x + B_x) i + (A_y +B_y) j         

C = (4.33 + 5) i + (8.66-2.5) j

C = 9.33 i + 6.16 j                   

ب- نوجد مقدار المتجه C والزاوية التي يصنعها مع المحور السيني x

C = 11.18 m

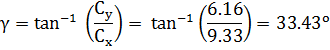
ت- نحدد الربع الذي تقع به المحصلة C

حيث أن المركبة السينية موجبة والمركبة الصادية موجبة, أذا يقع المتجه C  في الربع الأول.

ث- الإجابة تساوي

* للقيام بجمع أكثر من متجه, تكرر نفس العمليات السابقة بعدد المتجهات المجمعة.

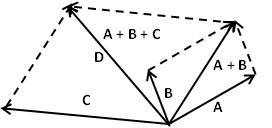
D = A + B + C

D = (A_x + B_x + C_x) + (A_y + B_y + C_y ) 

D = (A_x + B_x + C_x) i + (A_y + B_y + C_y ) j

D = D_x i + D_y j                                     

طرح المتجهات Vector subtraction:

تتم عملية الطرح بنفس عملية الجمع ولكن بعد تغيير اتجاه المتجه المطروح بحيث يكون اتجاه معكوس, يكون اتجاه السهم بالناحية الأخرى (يتغير اتجاه المتجه 180 درجة), ثم يتم جمع المتجهات

عملية الطرح مشابهة لعملية الجملع بحيث تعمل الإشارة السالبة إلى تغيراتجاه المتجه الثاني المراد طرحه, ثم يتم جمع المتجه الأول مع المتجه الثاني بعد تغييراتجهة.

ضرب المتجهات

Vectors multiplications (vectors product)

يمكن تقسيم ضرب المتجهات إلى التالي: ضرب المتجه في كمية قياسية, ضرب متجه في متجه. حاصل ضرب المتجه في كمية قياسية ينتج عنه متجه, له نفس الاتجاه, ومقداره يساوي مقدار المتجه مضروب في الكمية القياسية. أما ضرب المتجه في المتجه قد ينتج عنه كمية قياسية (الضرب القياسي) أو كمية متجه (الضرب الإتجاهي), وللتفريق بين عمليتي الضرب هاتين نستخدم رميزين مختلفين, يرمز للضرب القياسي (.), A . B. ويرمز للضرب الأتجاهي بعلامة الضرب (×), A x B.

1- ضرب المتجه في كمية قياسية (multiplication of a vector by a scalar):

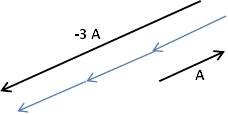
أ- ضرب المتجه في كمية قياسية موجبة يعمل على تغيير قيمة المتجه دون التأثير على اتجهه.

ب- ضرب المتجه في كمية قياسية سالبة يعمل على عكس اتجاه المتجه وتغيير قيمته.

مثال تطبيقي:

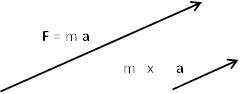
القوة = الكتلة x العجلة

حيث أن متجه القوة يساوي حاصل ضرب الكتلة (كمية قياسية) في متجه العجلة. آي أن متجه القوة يكون في اتجاه متجه العجلة ويكون مقداره يساوي مقدار العجلة مضاعف بمقدار القوة.

F = m a

2- ضرب متجه مع متجه (multiplication of a vector by a vector):

أ- الضرب القياسي dot product

سمى بالضرب القياسي للمتجهات لإن حصيلة الضرب تعطي كمية قياسية (قيمة عددية). وترتيب الضرب القياسي لا يغير قيمة محصلة الناتج, ولذلك فإن a.b = b.a

مثال تطبيقي:

الشغل work:

يعرف الشغل: بإنه (القوة مضروبة في الإزاحة(. وحيث أن القوة متجه والأزاحة متجه ولكن ضربهم يعطى قيمة قياسية وهي مقدارالشغل.

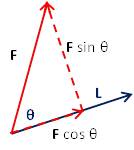
في حالة أن هناك زاوية بين متجه القوة ومتجه الإزاحة تساوي θ, فإن الشغل يساوي

W = F.L = F L cos θ

حالات خاصة

- في حالة أن متجه القوة في نفس اتجاه متجه الأزاحة يكون الشغل موجب (الزاوية بين المتجهين= صفر) cos 0 = 1,.

- في حالة أن متجه القوة عكس متجه الإزاحة يكون الشغل سالب (الزاوية بين المتجهين = 180^o “π”) cos 180 = -1,.

- في حالة أن متجه القوة عمودي على متجه الإزاحة فيكون الشغل الناجم من هذه القوة يساوي صفر(الزاوية بين المتجهين  = 90^o ”π/2”)cos 90 = 0, . 

تحلل مركبة متجه القوة F إلى مركبتيين متعامدان أحدهما في أتجاه متجه الإزاحة L والاخري عموديه عليه. من الرسم فإن مركبة متجه القوة التي في نفس اتجاه الإزاجة تساوي F cos θ تعطي شغل يساوي F L  cos θ, والمركبة الأخري للقوة العمودي F sin θ تعطي شغل يساوي صفر. وعليه يكون مجموع الشغل الناتج من متجه القوة يساوي مجموع شغل المركبتين, يساوي W = F.L = F L cos θ.

الضرب القياسي للمتجهات في الصورة الكرتيزية:

عند ضرب المتجات i.i = 1, j.j = 1, k.k = 1 حيث أن مقدار كلا منهم يساوي واحد, حيث أن الزاوية بين متجه الوحدة وشبيه تساوي صفر.  وحاصل الضرب لمتجهي الوحدة المتعامدين يساوي صفر حيث أن cos 90 = cos -90 = 0 ويكون k.i = k.j = j.i =k.(-i) =… = 0.

وعند تطبيق ذلك بضرب المتجهين a.b = (a_x i + a_y j + a_z k) . (b_x i  + b_y j + b_z k)  

فإن كلا من المتجهين a, b له ثلاث مركبات في الأتجاهات المتعامدة x, y, z, فعند أجراء الضرب يتم ضرب متجه مركبة المتجه a_x في الثلاث متجهات لمركبات المتجه  bضرب قياسي, وحيث أن a_x تكون في نفس اتجاه المركبة b_x فقط ومتعامدة مع متجهي المركبتين b_x, b_y, فإن حاصل الضرب يساوي مقدار قياسي يساوي a_x b_x + 0 + 0, أي يساوي a_x b_x. وبالمثل لباقي متجهات مركبة المتجه a, فيكون حاصل الضرب القياسي للمتجه a.b يساوي التالي:

a.b = (a_x i + a_y j + a_z k) . (b_x i  + b_y j + b_z k) = a_x b_x + a_y b_y + a_z b_z

مثال تطبيقي:

ما هو مقدار الشغل الناتج من قوة مقدارها F = (4 i + 3 j – 5 k) N, لجسم حدثت له إزاحة مقدارها m L =( 6 i – j + 2 k).

الشغل w يساوي
w = 4X6 – 3x1 - 5x2 =  11 J

ب- الضرب الاتجاهي cross product:

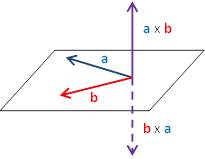
الضرب الأتجاهي يستخدم علامة الضرب "×"  بين المتجهين. وينتج من ضرب المتجهين متجه ثالث يكون عموديا على مستوى المتجهين الأصليين. كما يبين الشكل عند ضرب المتجه a في المتجه b ينتج متجه axb عمودي على المستوى الواقع به المتجهين الأصليين a, b.

ويكون مقدار المتجه العمودي يساوي:

|c | =| a x b |= a b sin θ

حيث θ هي الزاوية الصغرى بين المتجهين a, b. في حالة أن المتجهين في نفس الاتجاه يكون مقدار المتجه c يساوي صفر, وفي حالة أن الزاوية بينهما 90^o فإن مقدار المتجه c يكون مقداره axb.

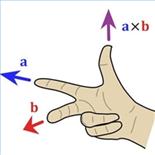
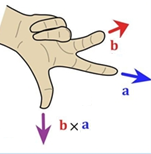
لمعرفة اتجاه المتجه c نستخدم قاعدة اليد اليمنى, حيث يشير السبابة إلى أتجاه أحدى المتجهين وليكن a, ويشير الإصبع الأوسط إلى المتجه الأخر b, فإن حاصل الضرب يكون متجه ويكون اتجاهه كما يشير إليه الإبهام (كما في الشكل التالي). ترتيب الضرب عكس اتجاه دوران عقارب الساعة ناحية الزاوية الصغيرة المتكونة بين المتجهين.

وعليه نجد أن ترتيب الضرب الاتجاهي مهم حيث أن:
a x b ≠ b x a

الضرب الاتجاهي للمتجهات في الصورة الكارتزية:

عند الضرب المتجهي لمكونات المتجهات, فأن ضرب المكونات التي لها نفس الاتجاه تعطي صفر حيث أن الزاوية بين نفس الاتجاه تساوي صفر وعليه فإن الضرب الإتجاهي لأي متجهين لهم نفس الاتجاه يعطي متجه يساوي صفر كالتالي | c |=| a x b |= a b sin 0 = 0 .  وفي حالة ضرب إتجاهي لمتجهين بينهما 90^o يعطي متجها مقداره يساوي محصلة ضرب المتجهين ويكون عمودي على مستواهما, وعليه فإن مقدار ضرب المتجهات التالية a x b يساوي

a b sin 90 = a b, كما أن ضرب المتجهين بترتيب مختلف يعطي:

| c |= |b x a | = a b sin (-90) = - a b . بتطبيق هذا على المركبات الكرتيزية فإن:

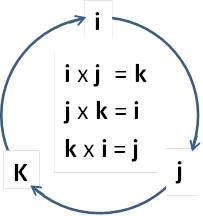
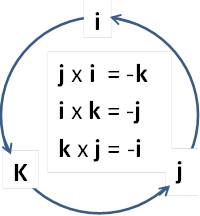
i x i = 0, j x j = 0, k x k = 0, ويمكن تمثيل الضرب الاتجاهي لمتجهات الوحدة حسب الترتيب كما في الشكل:

مثال:
اوجد حاصل الضرب الاتجاهي للمتجهين a, b  حيث:

a = 3 i -3 j +k, b = 4 i + 9 j = 2 k

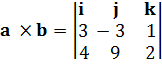
a x b = i (-3x2 – 9x 1)  -  j (3x2 – 4x1) + k (3x9- 4x-3)

a x b = -15 i - 2 j +39 k

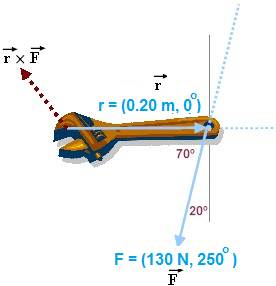
مثال تطبيقي:

في الشكل التالي, مفتاح عزم يستخدم لتربيط مسمار. مفتاح العزم يظهر كمتجه r والقوة المؤثرة كمتجه F. الضرب الاتجاهي للمتجهين r x F هو مقدار القوة المؤثرة على المفتاح. القوة  F تؤثر بزاوية مقدارها 250^o . الزاوية بين المتجهين r , F تساوي θ = 180- 110 = 70^o. حيث sin 70 = sin 110 . وعليه يكون مقدار العزم يساوي

r x f = (0.20) (130) sin 70 = 24. 432 N m

بكتابة المتجهات في الصورة الكرتيزية:

r = 0.2 i, F = 130 cos 250 i + 130 sin 250 j = - 44.463 i - 122.16 j

وعليه فيكون العزم يساوي

T = r x F = 0.2 i x (-44.463 i – 122.16 j ) = - 24 .43 k

اتجاه هذا المتجه عمودي على المستوي المتواجد فيه كلا r, F وهو (-z) وهو ما يسمح بتربيط المسمار. 

هناك الكثير من الأمثلة التطبيقية على الضرب المتجهي للمتجهات مثل: القوة المؤثرة على سلك يمر به تيار داخل مجال مغناطيسي (نظرية عمل الموتور الكهربائي), أو مقدار التيار المار في سلك نتيجة قطع السلك لخطوط المجال المغناطيسي (نظرية عمل المولد الكهربائي).

- المتجه بين نقطتين vector between two points:

يمكن تمثيل المتجه الذي يصل بين نقطتين  (x₁,y₁) , (x₂, y₂)عن طريق سهم يصل بينهما. وتكون معادلة المتجه كالتالي B = (x₂- x₁) i + (y₂- y₁) j, حيث B هو متجه يتجه من نقطة (x₁, y₁) إلى نقطة (x₂, y₂).

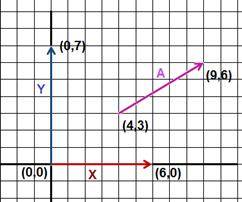
مثال:
أوجد المتجه X الذي يصل نقطة الأصل (0,0) مع النقطة (6,0)
أوجد المتجه Y الذي يصل نقطة الأصل (0,0) والنقطة (0,7)
أوجد المتجه A الذي يصل النطقتين (4,3), (9,6)

X = (6- 0) i + (0-0) j = 6 i

X = 6 i                              

وطوله يساوي 6 ويصنع زاوية صفر مع المحور السيني (θ = tan^-1 (0/6) = 0^o)

Y = (0-0) i + (7-0) j

Y = 7 j                    

وطوله يساوي 7 ويصنع زاوية 90 درجة مع المحور السيني (θ = tan^-1 (7/0) = 90^o)

A = (9-4) i +(6-3) j

A = 5 i + 3 j

وطوله يساوي ,                                                    

ويعمل زاوية مع المحور السيني تساوي (θ = tan^-1 (3/5) = 31^o)

تمثيل المتجه في الأبعاد الثلاثة (المركبات):

a = a_x + a_y + a_z

a = a_x i + a_y j + a_z k

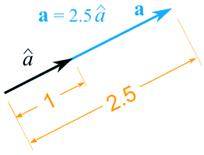
- متجه الوحدة unit vector:
متجه الوحدة هو متجه طوله يساوي 1 (وحدة الاطوال). ويرمز لمتجه الوحدة في العادة بحرف (من الحروف الصغيرة ويوضع عليه الرمز ^{^},lower case letter with (ˆ)  . حيث يمثل â متجه الوحدة.  متجه الوحدة â يساوي المتجه a مقسوم على طوله.

ويستخدم متجه الوحدة ليحدد اتجاهات كمية المتجهات في محاور عدة. في المحاور الكارتيزية فإنه يستخدم أحد الحروف i, j, k لمتثيل متجه الوحدة في الاتجاه السيني أوالصادي أوالعيني x, y,z بالترتيب.

مثال:

- أوجد متجه الوحدة للمتجه A = 10 i
حيث أن طول المتجه يساوي 10 فإن متجه الوحدة يكون  = i â

- أوجد متجه الوحدة للمتجه B = 3i + 4 j –12k
طول المتجه B يساوي 
B = 13,

ويكون متجه الوحدة b = 3/13 i  + 4/13 j + 12/13 k
b = 0.231 i + 0.308 j - 0.923 k هذا هو متجه الوحدة في اتجاه المتجه B.

عند حساب طول متجه الوحدة b نجده يساوي , يساوي 1

ويكون المتجه B = 13 b, حيث 13 طول المتجه B و b هو إتجاه المتجه B.

تطبيقات مختلفة:

تمثيل المتجه:

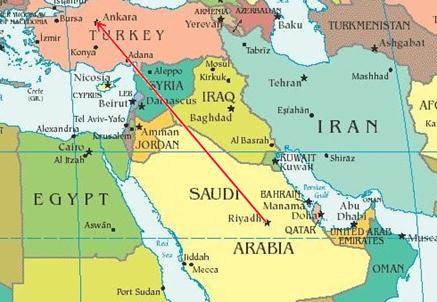
يرسم المتجه بمقياس رسم مناسب لتمثيل المتجه الأصلي, ويقصد بمقياس الرسم 1: 1000 مثلا أن كل وحدة قياس للمتجه المرسوم تساوي 1000 من نفس وحدة القياس للمتجه الأصلي.

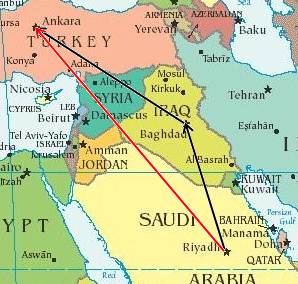
وعليه يمكن تمثيل المسافة من الرياض إلى أنقرة والتي تساوي 2081 كم أي (2.081x 10⁸ cm) بمتجه طوله 10.40 cm وهنا يكون مقياس الرسم 1: 20 000 000  أو رسمه بمقدار 5.20 cm  الذي يقدر بمقياس رسم 1: 10 000 000 ويختار مقياس رسم المتجه حسب مساحة ورقة الرسم المتاحة ودقة الرسم المطلوبة.

مثال:
يمكن تمثيل رحلة طيران من الرياض بالمملكة العربية السعودية إلى بغداد بالعراق بالمتجه الأول ثم من بغداد إلى انقرة بتركيا بالمتجه الثاني. ويكون مجموع المتجهين يساوي المتجه من الرياض إلى أنقرة. يشترك المتجه من الرياض إلى أنقرة مع المتجه الأول في نقطة البداية (الرياض) ومع المتجه الثاني في نقطة النهاية (أنقرة). ويرسم المتجه بمقياس رسم كما هو موضح بالشكل.

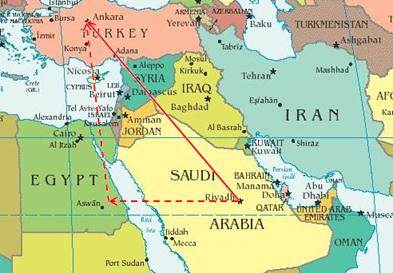
مثال:

تحليل المتجه كما هو مبين بالشكل المتجه من الرياض إلى أنقرة يعني أن الرحلة هي مجموع حيث تقع أنقرة  في الشمال الغربي من الرياض مسافة  1351 km غربا ,مسافة 1583 km شمالا.

ويمكن تمثيل المتجه من الرباض إلى أنقرة بالمتجهين متجه في اتجاه الغرب والمتجه الأخر في إتجاه الشمال
A= (1351 km) west + (1583 km) north

. في حالة تمثيل المتجه بالمحاور الكرتيزية فإن الغرب يكون - i والشمال j .

= -1351 i +1583 km j = 2081 km المسافة بين الرياض وأنقرة

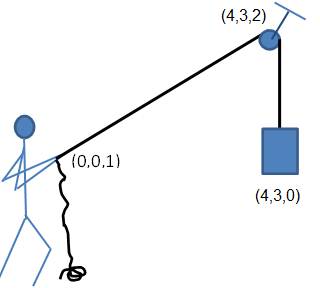
مثال:
يرفع رجل حمل مقداره 400 نيوتن ويستخدم حبل مع بكرة مثبته في حامل, كما في الشكل.

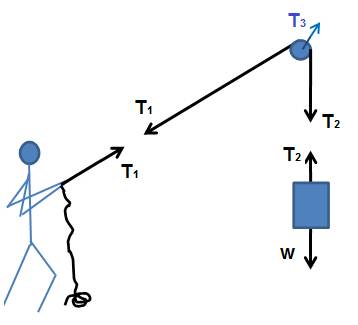
أ- اوجد متجه القوة المبذولة من الرجل, ومقدار القوة في الحبل الرئسي

ب- مقدار المحصلة للحبل المثبت للبكرة

جـ- مقدار الشغل المبذول لرفع كتلة مقدارها  1.2 متر

أ- مقدار الشد في الحبل الرأسي يساوي T₂, T₂ = 400 N, ومع أهمال الاحتكاك في البكرة يكون الشد في الحبل

المائل يساوي نفس قيمة الشد في الحبل الرأسي, (حبل واحد), T₁= 400 N.

متجه الحبل المائل في اتجاه قوة الشد يساوي L₁, ويتجه من نقطة 2: (4,3,2) إلى نقطة 1: (0,0,1)
L₁= (x₁-x₂) i + (y₁- y₂) j + (z₁-z₂) k

L₁= (0-4) i + (0-3) j +(1-2) k

L₁= -4 i -3 j - k

طول الحبل المائل =

L₁ = 5.1m

متجه الوحدة في الحبل المائل يساوي

 ويكون متجه القوة في الحبل المائل يساوي مقدار قوة الشد مضروب في متجه الحبل

متجه القوة في الحبل الرأسي يساوي مقدار الشد = 400 N, مضروب في متجه الوحدة في اتجاه الشد = - k

T₂ = 400 x ( – k)

T₂ = - 400 k

ب- مقدار المحصلة T₃ لحبل البكرة يساوي محصلة T₁, T₂

T₃ = T₁ + T₂

جـ - مقدار الشغل بالنسبة T₂ لرفع الوزن لمسافة 1.2 m يساوي حاصل ضرب الشد في مسافة رفع الوزن

مقدار الشغل بالنسبة T₁ شد لمسافة 1.2 m , حيث متجه الخط المائل لمسافة 1.2 m يساوي متجه الوحدة للحبل المائل مضروب في 1.2

ويكون مقدار الشغل هو حاصل الضرب القياسي لمتجه الشد في الحبل المائلT₁ ومتجه الحبل المائل L

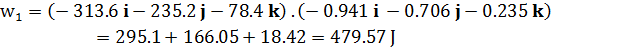
كما يظهر من الحسابات أن w₁ = w₂ أي أن الشغل لرفع الوزن لأعلى رأسيا يساوي الشغل لجذب الحبل المائل لنفس المسافة.