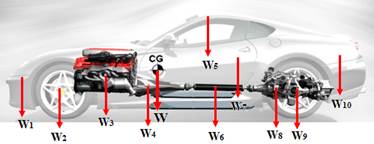
Finding the Car Center of Gravity/Mass (CG/CM)

What is mint by the center of gravity?
Center of gravity, also known as center of mass, is that point at which a system or body behaves as if all its mass were centered at that point. Where the weight, and also all accelerative forces of acceleration, braking and cornering act through it.

Center of gravity location can be defined as:
- The balance point of an object
- The point through which a force will cause pure translation
- The point about which gravity moments are balanced (see Fig.1)
- The point which if the body is hanged from it will stay balanced (leveled as it is on the ground).

Fig. 1 Summation of moments of parts weights around any point is equal to the moment of the summation of weights around this point. W. X_CG = (W₁.X₁+ W₂. X₂ + W₃. X₃ + W₄. X₄ + W₅. X₅ + ……..)

X_CG = Σ (W.X) / Σ (W), where X_i is the distance in x direction between the point i and that point.

What is the importance of the CG?
When making an analysis of the forces applied on the car, the CG is the point to place the car weight, and the centrifugal forces when the car is turning or when accelerating or decelerating.  Any force that acts through the CG has no tendency to make the car rotate.

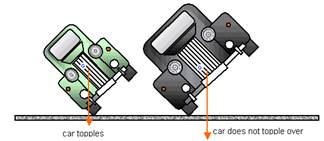
The center of mass height, relative to the track, determines load transfer, (related to, but not exactly weight transfer), from side to side and causes body lean. When tires of a vehicle provide a centripetal force to pull it around a turn, the momentum of the vehicle actuates load transfer in a direction going from the vehicle's current position to a point on a path tangent to the vehicle's path. This load transfer presents itself in the form of body lean. Body lean can be controlled by lowering the center of weight or the widening the car track, it can also be controlled by the springs, anti-roll bars or the roll center heights.

Fig.2 Increasing the height of the CG or decreasing the width of the car track will cause the car to topple.

The center of mass height, relative to the wheelbase, determines load transfer between front and rear. The car's momentum acts at its center of mass to tilt the car forward or backward, respectively during braking and acceleration. Since it is only the downward force that changes and not the location of the center of mass, the effect on over/under steer is opposite to that of an actual change in the center of mass.

A lower center of mass is a principal performance advantage of sports cars, compared to sedans and (especially) SUVs. Some cars have body panels made of lightweight materials partly for this reason.

Obtaining the position of the car CG:
A vehicle is not symmetrical in shape or mass from front to rear. Most vehicles are symmetrical left to right in shape but not in mass, especially front wheel drive vehicles.

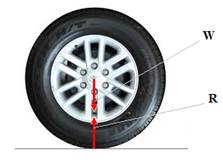
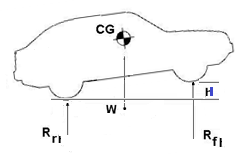
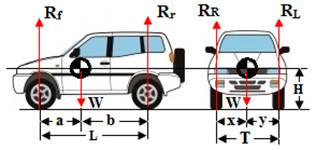
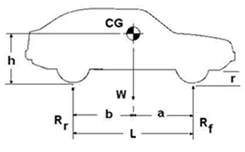
Fig. 2 Weight (W), Reaction (R)	Fig. 3 The CG location in the side and front view

The difference between weight W and Reaction R: 
From Fig.2, W is the weight of the tire (always vertical and downward) , while R is the reaction from the ground (always perpendicular to the ground surface and away from it).  The tire is balanced in the vertical direction under its weight (W) and the ground reaction (R), that means the summation of forces in that direction is zero (W – R = 0), which gives W = R.
In our analysis we measure the weights, but when studding the car balance we use the reactions supporting the car from the ground (where: W_f  = R_f, W_r = R_r, W_w = R_w and W_L = R_L).
The symbols in Fig. 3 are donated to:
W is the car weight,
R_f is the ground reaction of the frontal axle weight
R_r is ground reaction of the rear axle weight
R_R is ground reaction of the car right wheels weight
R_L is ground reaction of the car left wheels weight
L is the car wheel base (distance between the front and rear car wheels/axles)
T is the car track (distance between the center of the wheels on the same axle)
a is the location of the CG behind the front axle
b is the location of the CG in front of the rear axle
x is the location of the CG away from the right wheels
y is the location of the CG away from the left wheels

A. The longitudinal location of CG:

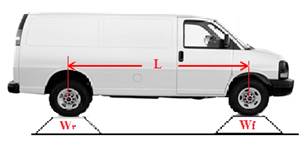
Fig. 4 Measure the front and rear axle weights (Wf ,Wr), and the wheel base length (L)
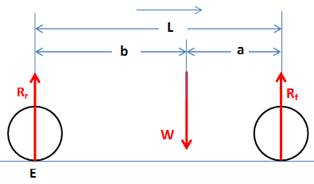
Fig. 5 The car on a level surface, L is the wheel base, the front and rear axles wights (Wf, Wr) and (a and b are unknown longitudinal distances of the CG)

*Measure the wheel base, L (the distance between the center of the front and rear wheels), Fig. 3

L = a +b ……………………………………………….(1)

a = L – b ……………………………………………….(2)

Σ F_y = 0

W – (R_f + R_r) = 0 ………………………………………(3)

Then W = (R_f + R_r) …………………………………….(4)

* Measure the car front axle weight W_f = R_f, and the car rear axle weight W_r = Rr, Fig. 3.

Use equation (4) to find the car weight W.

Take moment around point E.

Σ M_E = 0

R_f  L – W b = 0

R_f  L= W b, then

b = L (R_f/W) ………………………………….…………(5)

Use eq. (5) to find the distance b.

Substitute the value of b in eq. (2) to get the distance a.

* In Eq. 5, the units of R_f and W can be expressed in unit force (N, lb) or unit mass (kg), the units of L and b can be expressed in (m, cm, mm, or ft, in).

B. The height above ground of CG (h):

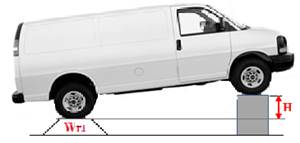
The weight of the rear axle (W_r1) will be weighed while the front pair of wheels are raised up quite a small distance H (or h₁) (as shown in figure 6).

Fig.6 Measure the rear axle weight (Wr1) and the distance of front raise (H)
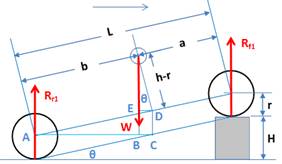
Fig. 7 The front wheels are raised up a small distance H (h1), r is the wheel radius, (h is the unknown distance of the CG height)

Using Fig. 7:

The summation of vertical forces in the y direction is equal 0.

Σ F_y = 0

R_f1 + R_r1 – W = 0

Then:  R_f1 = W – R_r1

The summation of moments about any point is equal 0, then:

Σ M_A = 0

R_{f 1} (L cos θ) - W (AB) = 0

R_{f 1} (L cos θ) = W (AB) ……………………………….(6)

From the figure:

AB = AC – BC,

Where:

AC = b cos θ, and

BC = ED = (h-r) sin θ,

Then:

AB = AC – BC = b cos θ – (h-r) sin θ

Substitute the value of AB form the above equation in Eq. (6), then

R_f1 (L cos θ) = W (b cos θ – (h-r) sin θ)

R_f1 (L cos θ) = W b cos θ –  W (h-r) sin θ

W (h-r) sin θ = W b cos θ –  R_f1 (L cos θ)

h– r = [b – L (R_f1/W)] cot θ …………………………..(7)

h = [b – L (R_f1/W)] cot θ + r ………………………….(8)

where:

θ = sin^-1 (H/L)

(h-r) is the distance of CG above the axle plane, Eq. (7)

h is the distance of CG above the ground, Eq. (8)

* In Eq. 8, the units of R_f1 and W both can be expressed in unit force (N, lb) or unit mass (kg), the units of b, L, r and h can be expressed in (m, cm, mm, or ft, in).

An Excel program to Obtaining the center of gravity location (a,b, and h)

       C. The side location of CG:

         The right and left wheels weights (W_R, W_L) will be measured and the car track T.

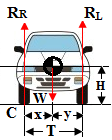
Fig. 8 Finding the CG position in the frontal view, distance x, y.

The car load balance in vertical direction shows:

W = W_R + W_L

Taking moment about point C will get the distance x

Σ M_C = 0,

W.(x) – R_{L .} (T) = 0

x = (R_L/W) T,

y = T – x

Most cars except the front wheel drive are symmetric in weight distribution in the front view (R_R = R_L). So that the CG position will be in the middle (x = y = T/2). In most cars it is a fair approximation to assume that.

Worked example:

A vehicle having a mass of 2000 kg and a wheelbase of 2.44 m, the car center of gravity lies1.52 m from the rear axle. The front end of the vehicle is lifted 35 cm and gives a mass reading of 1150 kg. The wheel radius is 30.5 cm. Determine the height of the CG.

Required

h

Given:

m = 2000 kg

L = 2.44 m

b = 1.52 m

H = 35 cm

R_f1 = 1150 kg

r = 30.5 cm

Answer:

θ = sin^-1 (H/L) = sin^-1 (35/244) = 8.247

cot θ = 6.899

h = [b – L (R_f1/W)] cot θ + r

h = [1.52 – 2.44 (1150/2000)] 6.899 + 30.5

h = [1.52 – 1.403] 6.899 + 0.305 = 0.807 + 0.305

h = 1.112 m

Source: thecartech@yahoo.com