Setting the Gearbox and Final Drive Ratios

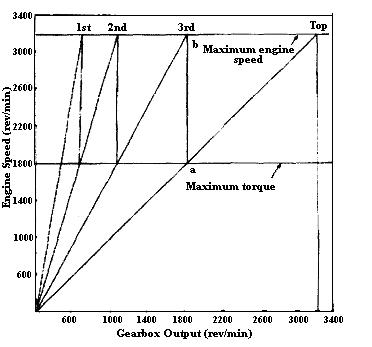
A method of showing an engine’s speed ratio is given in the figure. This is based on the assumption that engine revolutions should not fall below the speed of maximum torque. The point at which the top gear line crosses the maximum torque line is the point at which a gear change should be made. The change is indicated by a vertical line ab, and the line drawn from b to the origin 0 represents the conditions after the change down. The process is repeated for the other ratios. The horizontal distance between the vertical lines increase in geometrical progression or approximately to this (depending upon whether modifications to some or all the calculated ratios has been made).

Top gear ratio = 3200/3200 = 1 to 1

3^rd gear ratio   = 3200/1800  = 1.77 to 1

2^nd gear ratio   =  3200/1100 = 2.91 to 1

1^st gear ratio    = 3200/740    = 4.325 to I

Engine speed ratio = 1800 / 3200 = 0.5625

Note: that in the above gear settings, first gear has been lowered slightly out of geometrical progression with second, and third gear moved closer to top gear, hence the speed ratio 0.5625 would not now apply.

Worked example (calculating the possible gear ratios for a vehicle):

Calculate the gear and final drive ratios for a vehicle from the given data:

Maximum engine torque is 105.2 N m at 2100 rev/mm. Maximum power is 37.3 kW at 4000 rev/mm, giving a road speed of 130 km/h obtained from graphs and data. The rolling radius of road wheels is 0.366 m. Transmission efficiency is 90% and the maximum tractive resistance is 4890 N.

v = 0.377 R_w N_w = 0.377 R_w N_e/ (i_g  i_f)

v_max = 0.377 R_w N_w = 0.377 R_w N_{e max}/ (i _{Top gear} i_f)

i_f = 0.377 R_w N_{e max}/(i_{Top gear} v_max) = 0.377 x 0.366 x 4000 / (1 x 130) = 4.245 : 1

Maximum tractive resistance = maximum tractive effort in bottom gear

TR_max = T_{e max}  i_g i_f η_t / R_w

i_g = TR_max x R_w /(T_{e max}  i_g i_f η_t)

= 4895 x 0.366/(105.2 x 4.245 x 0.9) = 4.458:1

Engine ratio (K) = N_{e (max torque)} / N_{e max} = 2100 / 4000 = 0.525

i_g1 = K^n-1 i_g1 = K^1-1 i_g1 =K⁰ i_g1 = 1 x 4.458 = 4.458

i_g2 = K^n-1 i_g1 = K^2-1 i_g1 =K¹ i_g1 = 0.525 x 4.458 = 2.34

i_g3 = K^n-1 i_g1 = K^3-1 i_g1 =K² i_g1 = (0.525)² x 4.458 =1.228

Worked example (tractive effort and tractive resistance):

A vehicle has a torque of 480 N m applied to its driving wheels. Rolling resistance is 320 N. If the vehicle has a mass of 1780 kg what propelling force will be available to accelerate the vehicle while it is climbing a gradient of 1 to 20. The rolling radius of the road wheels is 0.3 m. What is the maximum acceleration of the vehicle at this speed?

w = mg = 1780 x 9.81 = 17461.8 N

GR = w sin θ = 17461.8 x (1/20) = 873 N

TE = T_w / R_w = 480/0.3 = 1600 N

TR = RR + GR = 320 + 873 = 1193 N

SE = TE – TR = 1600 – 1193 = 407 N

SE = ma

a = SE / m = 407/ 1780 = 0.229 m/s²

Homework

1) Set the final drive and the gear ratios for a vehicle, given the following data:

Maximum engine torque is117 N m at 2000 rev/min. Maximum engine power is produced at 4200 rev/min, which gives maximum road speed of 144 km/h. The maximum tractive resistance (TR) is 6230 and the transmission efficiency at bottom gear (η_t) is 80%. Rolling radius of the wheels (R_w) is 0.365 m.

2) An engine producing a torque of 352 N m is fitted to a vehicle of mass 1670 kg has a 4.35 final drive ratio giving a transmission efficiency of 80%. The rolling resistance is 356 N and the effective wheel diameter is 0.62m. If this