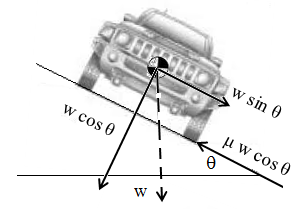
أقصى زاوية ميل جانبي يمكن للسيارة السيرعليها   Side-slope angle (lateral slope)

قدرة السيارة على السير على طريق مستقيم (ليس به انعطاف) له ميل جانبي يعتمد على تغلبها على عاملين. العامل الأول هو انزلاق السيارة. العامل الثاني هو انقلاب السيارة.

معامل التلاصق بين الإطارات والطريق (انزلاق السيارة). ومع فرض أن معامل التلاصق μ ذو قيمة عالية فإن اقصى ميل جانبي يمكن للسيارة السير عليه يعتمد على أبعاد السيارة: المسافة بين العجلات track L و ارتفاع مركز ثقل السيارة  center of gravity h. وتكون أقصى زاوية ميل للسيارة هي  θ = tan^-1 (2h/L).
لم يأخذ في المعادلة السابقة الاعتبار رخاوة الارض, ليونة الإطارات, نظام التعليق, كذلك سرعة السيارة أثناء الدخول في منعطف (القوة الطاردة المركزية). تم اعتبار أن مركز ثقل السيارة يقع في منتصف السيارة L/2.
قيم زاوية أقصى ميل جانبي للسيارات الرياضية ومركبات خارج الطريق يتم التوصل إليها عن طريق اختبار السيارة.

حد الانزلاق  w sin θ > μ w cos θ tan θ > μ	حد الإنقلاب(w cos θ)  L/2  w sin θ  h > tan θ > 2h/L
في حالة أن (μ < 2h/L)  فإن احتمال انزلاق السيارة  اكبر من انقلابها, في حالة وجود زيت على الطريق (يقلل من قيمة معامل الاحتكاك) فإن ذلك يزيد من احتمال انزلاق السيارة	في حالة أن (μ > 2h/L)  فإن احتمال انقلاب السيارة أكبر من انزلاقها
لا يحدث انزلاق أو انقلاب للسيارة في حالة أن في حالة أن θ أقل في المقدار من قيمة أي من المقدارين [tan^-1(μ), tan^-1(2h/L)]
حيث: μ = معامل التلاصق بين الإطار والطريق θ = زاوية الميل الجانبي للطريق h = ارتفاع مركز ثقل السيارة L = المسافة بين العجلات (الأثر) w = وزن السيارة # المعادلات السابقة لا يدخل فيها تأثير مرونة الإطار ولا يدخل فهيا تأثير نظام التعليق والنوابض ورخاوة الطريق. * يلاحظ أن المعادلات السابقة تأثير وزن السيارة أو حمولتها لا يدخل فيها بشكل مباشر ولكن الحالة تعتمد فقط على قيمة معامل التلاصق بين الأطار والطريق μ, وابعاد السيارة (h, L). + قيمة معامل التلاصق لا تؤدي إلى انقلاب السيارة¸ ولكن انخفاض قيمتها قد يؤدي إلى انزلاقها قبل انقلابها, وزيادة قيمتها تمنع  انزلاقها, وقد تنقلب (حسب قيم ابعاد السيارة L,h و زاوية ميل الطريق الجانبية θ)

مثال: سيارة ارتفاع مركز ثقلها h = 0.6 m, والمسافة بين العجلات L= 2.4 m

أ- أي الاحتمالين أكبر انزلاق السيارة أم انقلابها في حالة السير على طريق معامل الاحتكاك μ = 0.4

     ب- في حالة السير على طريق مائل بزاوية 30^o ومعامل الاحتكاك μ = 0.6 ماذا سيحدث للسيارة

    جـ- ما قيمة زاوية ميل الطريق التي لا تنزلق أو تنقلب السيارة عليها في حالة أن معامل الاحتكاك للطريق μ = 0.6

     د- ما قيمة معامل الاحتكاك الذي سيؤدي إلى انزلاق السيارة, وما قيمته لانقلاب السيارة على طريق زاوية ميله θ= 20^o

أ- حيث أن قيمة:  2h/L = (2x0.6)/2.4 = 0.5   اكبر من معامل الاحتكاك μ = 0.4
فإن احتمال انزلاق السيارة أعلى من احتمال انقلابها عند سيرها على طريق مائل

ب- حيث أن قيمة tan θ = tan 30 = 0.57735   اكبر من قيمتي 2h/L = (2x0.6)/2.4 = 0.5 μ = 0.4,
فإن السيارة فإن السيارة معرضة للانزلاق والانقلاب (ولكن السيارة ستنزلق في تلك الحالة قبل انقلابها لقيمة μ المنخفضة عن 2h/L)

جـ - قيمة زاوية الطريق التي ستنزلق عندها السيارة θ₁ = tan^-1 0.6 = 30.9638^o, لقيمة معامل تلاصق μ = 0.6
قيمة زاوية الطريق التي ستنقلب عندها السيارة θ₂ = tan^-1 (2h/L) = tan^-1 (2x0.6)/2.4 = tan^-1 0.5 = 26.5650^o
حيث أن زاوية الانقلاب للطريق أقل من زاوية الانزلاق للطريق θ₂ = θ₂
فأن زاوية الطريق التي لا تنزلق أو تنقلب عندها السيارة θ < 26.565^o, عند زيادة الزاوية عن 26.565^o فأن السيارة ستنقلب قبل أن تنزلاق

د- حيث ان tan θ = tan 20 = 0.3640
فإن السيارة ستنزلق في حالة أن معامل الاحتكاك μ < 0.3640
حيث أن حد الانقلاب هو θ = tan^-1 2h/L = tan^-1 0.5 = 26.565^o >20^o , فأن السيارة لن تنقلب لأي قيمة لـ μ

العلاقة بين زاوية الميل الجانبي والنسبة المئوية للميل:

تقاس زاوية الميل الجانبي بالنسبة المئوية (%) أو بالدرجات θ^o, كما يظهر في الشكل التالي:

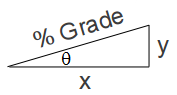
النسبة المئوية لميل الطريق الجانبي هي التغيير في مقدار الارتفاعy  المصاحب لمسافة أفقية x , مقسومة على نفس المسافة الأفقية x بحيث(Grade = y/x) . والزاوية هي (θ = tan^-1 (y/x). وتكون العلاقة بين النسبة المئوية للميل % وزاوية الميل θ كالتالي:

% Grade = (tan θ × 100) % = (y/x × 100) %

θ = tan^-1 (Grade /100) = tan^-1 (y/x)

أي أن زاوية 45^o تكون: = (1 × 100 ) % = 100 %  % Grade = (tan 45 × 100) %

و ميل 40% يكون: θ = tan^-1 ( Grade / 100) = tan^-1 (40/100) = tan^-1 (0.4) = 21.8^o

* السيارات العريضة (ذات مسافة كبيرة بين العجلات - الاثر), والتي لها مركز ثقل منخفض, والمجهزة بنظام تعليق وإطارات تناسب ظروف العمل خارج الطريق تكون لها قدرة أكبر للسير على الطرق ذات الميل الجانبي, وتكون زاوية الميل الجانبي أو النسبة المئوية للميل الجانبي للسيارة ذات قيمة عالية.

** لا يوجد احتمال لانزلاق السيارة على الأرض الوعرة, ولهذا لا يؤخذ في الاعتبار احتمال الانزلاق, ويعتمد أقصى ميل جانبي للطريق يمكن للسيارة السير على حد الانقلاب, الذي يعتمد فقط على أبعاد السيارة وارتفاع مركز الثقل, وهو ما يذكر في كتيب مواصفات السيارة.