International system of units (SI)
The Système Internationale d'Unitès was adopted in 1960 as the title for an MKSA system based on the meter (m), the unit of length; the kilogram (kg), the unit of mass; the second (s), the unit of time; the ampere (A), the unit of electric current; the Kelvin (K), the degree of temperature; and the candela (cd), the unit of light intensity.
Associated with these basic units are a variety of supplementary derived units which are adopted worldwide.
Derived units
|
Physical quantity |
SI unit |
Unit symbol |
|
Force |
Newton |
N = kg m/s2 |
|
Work, energy, quantity of heat |
Joule |
J =Nm |
|
Power |
Watt |
W = J/s |
|
Electric charge |
Coulomb |
C =A s |
|
Electrical potential |
Volt |
V =W/A |
|
Electric capacitance |
Farad |
F =A s/V |
|
Electric resistance |
Ohm |
Ω = V/A |
|
Frequency |
Hertz |
Hz = s-1 |
Multiplying factors
|
Factor |
Prefix |
Symbol |
|
1000000 [106] |
mega |
M |
|
1000 [103] |
kilo |
k |
|
100 [102] |
hecto |
h |
|
10 [10 ] |
deca |
da |
|
0.1 [10-1] |
deci |
d |
|
0.01 [10-2] |
centi |
c |
|
0.001 [10-3] |
milli |
m |
|
0.000001 [10-6] |
micro |
μ |
Physical Quantities
Speed and acceleration
Speed is measured as meters per second (m/s), or sometimes more conveniently as kilometers per hour (km/h). Useful conversions are 1 m/s = 3.6 km/h and 0.278 m/s = 1 km/h). Acceleration or deceleration is the rate of change of speed. It is measured as meters per second per second or m/s2
An increase in speed from 36 km/h to 72 km/h during 4 s (that is from 10 m/s to 20 m/s) is an average acceleration of 2.5 m/s every second or 2.5 m/s2
If the speed increases from u m/s to v m/s during t seconds, then the average acceleration a m/s2 is given by
a = (v-u)/t m/s2
Acceleration due to gravity
In a vacuum all freely falling bodies, whatever their size, shape or mass, have the same acceleration at a given place. This acceleration, given the symbol g since it is due to the force of gravity, has the value of about 9.81 m/s2 at sea level near London, 9.78 m/s2 at the equator, and 9.83 m/s2 at the poles.
The acceleration of objects falling in the atmosphere depends on their wind resistance. For example, depending on the conditions, the human body reaches a terminal velocity of some 200 km/h, when the wind resistance equals the force of gravity and no further acceleration can occur. A motor vehicle is also subject to wind resistance.
Force
The force is a measurable influence tending to cause movement of a body (its intensity). The unit of force is Newton, 1 Newton is the value of a force which if exerted upon one kilogram gives it an acceleration of 1 m/s2.
F = ma
where
F = force (Newton)
m = mass (kg)
a = acceleration (m/s2)
There are different types of forces; external force, internal force, and reaction force.
Mass and weight
A 'body' contains a certain amount of stuff or matter called mass. The unit of mass is the kilogram (kg).The pull of earth -the force of gravity- acting on this mass is the weight of the body. Owing to its mass a body has inertia, that is, it resists being accelerated or decelerated and will remain at rest or continue moving at a uniform speed in a straight line unless acted upon by an external force.
W = mg
where W= the weight in Newton [N], m= the mass in kilograms [kg], g = the acceleration of falling body due gravity in meter per second square [m/s2]
Principle of moments
When a body is at rest or in equilibrium (a state of balance), the sum of the clockwise turning moments about any axis, real or imaginary, is equal to the sum of the anticlockwise moments about the same axis.
Were this not the case, the unbalanced moment would cause the body to rotate about the chosen axis.
As an example, a beam of negligible weight has loads as shown in the Figure and is pivoted at P so as to be in equilibrium. Taking moments about P:
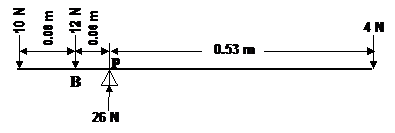 |
sum of anticlockwise moments = sum of clockwise moments
10 x (0.08 + 0.06) + 12 x 0.06 = 4 x 0.53
1.40 + 0.72 = 2.12
2.12 Nm = 2.12 Nm
The pivot P must exert an upward force on the beam equal to the sum of the downward forces of 10 N + 12 N + 4 N. This upward force of 26 N has no turning moment in this case since it is acting through the axis.
If we take moments about an imaginary axis at B, then:
sum of anticlockwise moments = sum of clockwise moments
10 x 0.08 + 26 x 0.06 = 4 x (0.53 + 0.06)
0.8 + 1.56 = 4 x 0.59
2.36 Nm = 2.36 Nm
The force of 12 N exerts no turning moment in this case as it is acting through the chosen axis.
Centre of gravity
The centre of gravity (CG) of a body can be regarded as the point where, if the whole weight of the body were concentrated, it would produce a moment of force about any axis equal to the sum of the moments of force of each part of the body about the same axis. When inertia force is involved the centre of gravity becomes the centre of mass.
As an example, consider a body consisting of weights of 10 N, 12 N and 4 N located on a beam of negligible weight, as shown in the Figure. Let L be the distance of the CG, of the body from an axis, say 0.01 m from the right-hand end of the beam. Taking moments about that axis:
Total weight of body (concentrated at CG) x distance of CG from any axis = sum of the moments of each part of the body about the same axis
(10 + 12 + 4) x L = 4 x 0.01 + 12 x 0.60 + 10 x 0.68
26 x L = 0.04 + 7.20 -t 6.80
L=14.04/26
L=0.54 m
The CG, is 0.06 m from the 12 N weight and 0.53 m from the 4 N weight, and this is the pivot point about which the body would balance.
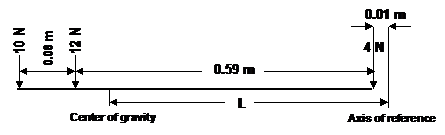 |
Couple
When two equal forces act on a body so that their lines of action are parallel but opposite in direction, they form a couple tending to rotate the body.
The torque produced by a force acting on a pivoted body can be regarded as the result of a couple formed by the original force and an equal and opposite reaction at the pivot (see the Figure).
|
A couple can only be balanced by another couple of equal value acting in the opposite direction of rotation and not by a single force. |
 |
Inertia force
All bodies have inertia -the tendency to remain at rest or in uniform motion. For example, when a piston is decelerated from maximum speed to a dead centre position and accelerated in the opposite direction, it exerts an inertia force on the connecting rod.
The value of the inertia force depends upon the mass of the body and
the acceleration or deceleration:
F = ma
where F= force in Newton (N), m = mass in kilograms (kg), and a = acceleration or
deceleration in meters/second/second (m/s2).
Thus to reduce the inertia forces produced by the reciprocating parts, their mass must be kept as small as possible.
Centrifugal force
A moving body travels in a straight line at uniform speed unless acted upon by an external force. If made to travel in a circle, the body exerts centrifugal force acting outwards from the centre upon the constraining member. The equal and opposite constraining force is termed centripetal.
CF = mv2/r
= mw2 r
where v = w r
where CF = centrifugal force in Newton (N), m = mass in kilograms (kg), r radius in meters (m), v linear velocity in meters/second (m/s), and w angular velocity in radians/second (rad/s), where 1 revolution = 2 p radians.
Free body diagram
1- Identify the object of interest.
2- Isolate the object of interest.
3- Draw the weight of the object as downward vertical force vector.
4- Identify all the individual interaction forces acting on the object, and draw them as force vectors on a free-body diagram.
5- Choose a convenient coordinate system, and draw the coordinate axles on the free body diagram.
6- Write the components of the vector equation in the chosen coordinate system (using the free body diagram).
7- Solve the equations for whatever quantities the problem asks for.
Equilibrium Equations
The body is considered in equilibrium state if the following equations are satisfied.
S Fx = 0
S Fy = 0
S Fz =0
S M @ any point = 0
where F = force, M= moment, and x, y, z are three arbitrary perpendicular axis.
CENTER OF GRAVITY (Center of mass)
All pieces of matter consist of a large number of molecules, each of which are a mass and subjected to the pull of gravity. All these forces are considered as being parallel to each other, and their resultant is the weight of the body. This acts through some point of the body. Thus the centre of gravity of a body is the point at which all forces or the weight of body is taken to act.
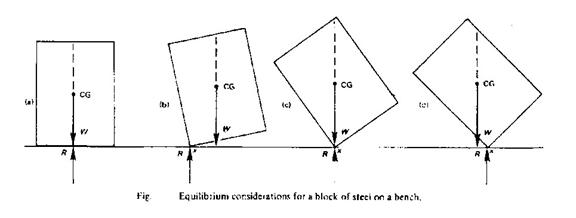
Types of equilibrium
Consider a block of steel (as shown in the figure) on a bench. In position (a) the block is in equilibrium and is considered to be in a stable condition. Its weight acting downwards is supported by the reaction of the bench. If the block is tilted as in (b) the block is acted upon by two forces, the reaction at the point of contact x and the weight W acting through the centre of gravity CG which will return the block to its stable position. If the block was tilted to a position (c) where W and the reaction R are equal and opposite, this would be considered as unstable equilibrium, and any further tilt would result in the force W acting to the left of the pivot point x (in the figure (d)). The block would then topple over. It may be noted that as the block is tilted from position (a) to position (c) the point of CG is rising and stable conditions exist, but beyond position (c) the CG begins to lower and unstable conditions exist.
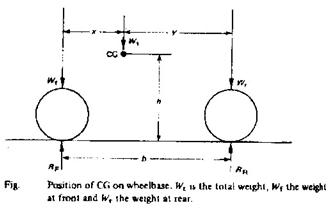
To determine the position of a vehicle's centre of gravity
Position of CG on wheelbase
| The weight of the vehicle must be known, and also the load carried by the front or rear wheels on a level surface. A vehicle weighbridge can be used. Moments can then be taken about the front or rear wheels.
Taking moments about RR:
RF . b = Wt . y and y = (RF . b)/ Wt
Therefore x = b-y |
 |
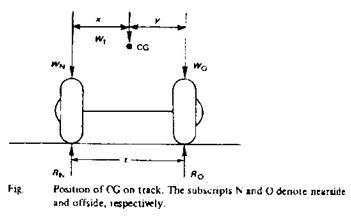
Position of CG on track
| The loadings on the nearside (RN) Or offside wheels (RO) must be known, then moments are taken about RN Or RO
Taking moments about the offside wheels RO (as shown in the figure):
RN . t = Wt . y
then y = RN . t / Wt
and t-y = x |
 |
To determine the height of a vehicle's CG: Method 1
The vehicle is placed on a tilting platform, and usually the road springs are made inoperative by wedging wooden blocks between the axles and the chassis. Ropes or chains are attached to the vehicle and platform for safety. The platform is tilted sideways until the vehicle is on the point of overturning sideways. A pointer and protractor will show the angle of tilt, or a clinometer may be used. Under these conditions the total weight or load line (Wt) will be passing through the centre of the loaded wheels contact area. If the CG is considered to be in the centre of the vehicle's track, therefore:
| tan q = (1/2 t)/ h
therefore
h = ((1/2) t) / tan q or h = t / (2 tan q) |
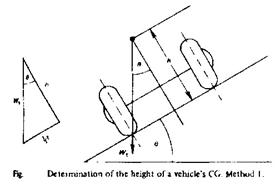 |
If CG is not in the centre of the track then the line of the CG and the outer or inner wheels distance will be substituted for (1/2) t.
Worked example (To determine the position of a vehicle's CG)
A vehicle having a total weight of 10 600 N carries 60% on its front wheels when on a level surface. The wheelbase is 3 m and track is 1.5 m .Calculate the position of the CG relative to the rear wheels.
RF = 0.6 of 10 600 = 6360 N
RF . b = Wt . y
therefore
y = RF . b / Wt = 6360 x 3 / 10600
y =1.8 m
Then x = b - y,
x = 3 - 1.8 =1.2 m
If this vehicle is at a point of balance when tilted through 42o, at what height lies the centre from the road surface?
h = t / (2 tan q) = 1.5 / (2 tan 42) = 0.833 m
I
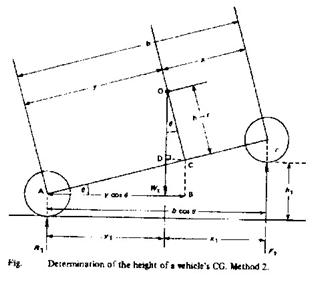
To determine the height of a vehicle's CG: Method 2
This method may be a little more difficult to understand, but if the rule of moments (force x perpendicular distance) is always applied, the calculations are quite easy. In practice no tilting platform is necessary, and only the axle loads are weighed while one pair of wheels are raised up quite a small distance h1 (as shown in figure). The angle is measured by a clinometer or protractor, and then moments may be taken, making sure the above rule is applied. Taking moments about point A:
| F1 (y1 +x1) = Wt . y1, From the figure y1 + x1 = b cosq and y1 = AB - CD = y cosq - (h-r) sinq (r is wheel radius) therefore Fl x b cosq = Wt . y1 = Wt (y cosq - (h-r) sinq) = Wt . y cosq - Wt .(h-r) sinq then Wt (h-r) sinq = Wt y cosq - Fl b cosq therefore (h-r) = (Wt y cosq - Fl b cosq)/(Wt sinq) If masses are given they can be used instead of weights, i.e. mass moments. |
 |
Worked example
A vehicle having a mass of 2000 kg has a wheelbase of 2.42 m and its center of gravity lies1.52 m from the rear axle. The front end of the vehicle is lifted 35 cm and gives a mass reading of 1150 kg. The wheel radius is 30.5 cm. Determine the height of the CG.
In this case mass moments will be taken about the rear wheels
sinq = h1 /b = 0.35 /24.4 = 8.247o
cosq = 0.9896 and sin q = 0.1434
h-r = ( m cosq - Fl b cosq) / (m sinq)
= ( 2000 x 1.52 x 0.9896 -1150 x 2.44 x 0.9896) / (2000 x 0.1434)
= ( 3008 – 2777) / 286.8
= 0.8054 m
thus h = (h-r) + r
= 0.8054 + 0.305
=1.1104 m
Examples
Example 1
The lifting gear on a vehicle body is situated 2.890 m from the pivot. If the body contains two loads of 15 kN and 7.5 kN whose centers of gravity are 0.835 m and 1.932 m respectively from the pivot, calculate the vertical force required from the tipping gear to raise the body
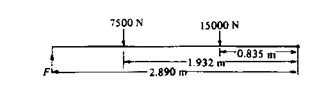 |
Neglecting the weight of the body, which is not given and taking moments about the pivot
Clockwise moment of tipping force = Sum of anticlockwise moments of loads
Let the required tipping force be F Newton. Then
F x 2.89 = 7 500 x 1.932 + 15 000 x 0.835
= 14 490 + 12 525
= 27 015 N m
F = 27 015 / 2.89 N
= 9347.75 N
= 9.348 kN
The required vertical tipping force is 9.348 kN
Example 2
A loaded vehicle of wheelbase 4.774 m is weighed by placing first the front wheels and then the rear wheels on weighbridge, the weights recorded being 9.236 kN and 12.792 kN respectively.
Calculate the position of the CG in front of the rear axle.
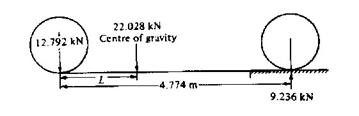 |
Let L be the distance of the CG in front of the rear axle. Then the force acting at L will be the total weight of the vehicle, which is the sum of the weights on front and rear wheels:
force at CG = 9.236 kN + 12.792 kN
= 22.028 kN
Consider the vehicle with the front wheels on the weighbridge. Taking moments about the rear axle:
clockwise moment = anticlockwise moment
22.028 x L = 9.236 x 4.774
= 44.093
Then
L = 43.093/ 22.029
= 2.002 m
The CG is 2.002 m in front of the rear axle.
Exercises
1. A vehicle having a total mass of 2.5 tonne carries 58% on the front wheels when the vehicle is on a level surface. The wheelbase is 3.2 m and track 1.6 m. Find the position of the centre of gravity relative to the rear axle and its height above the road surface if the point of balance on tilt test is at an angle of 46o. (1.856 m, 0.772 m)
2- A vehicle of total mass 5.6 tonne has a wheelbase of 4.3 m. On a level surface the centre of gravity lies 1.85 m from the rear axle at a height of 1.6 m. Determine the front and rear wheel reactions and the overturning angle if the centre of gravity is in the centre of the 2.2 m track. (RF = 2.4 tonne, RR = 3.19 tonne, 34.5o)
3- A vehicle having a total mass of 2800 kg carries 56% of this mass on its front wheels. The track is 1.46 m and wheelbase is 2.9 m. When on a tilt test the point of balance was reached an angle of 47o. Calculate the position of the CG from the rear wheels and the height above the road surface. (1.624 m, 0.68 m)