Center of Gravity and Moment Arm

You may have heard of the center of gravity, or center of mass, in geometry. We often talk about the centroid of a triangle as the center of gravity of the triangle — what this means is that if you cut a triangle out of stiff enough paper and found the centroid of the triangle (the intersection of the medians) you could balance that triangle on a pencil point placed at the centroid.

The Center of Gravity, often abbreviated CG, is the point on an object at which it is in perfect balance. If the object is something simple, with a uniform distribution of mass, the CG is at the geometric center of the object (e.g. the CG for a block would be at the center of the block); however, if the object is not uniform (say, a race car), the CG has to be found other ways and may not be in the exact center of the object. The CG is important because the CG is point at which we can take gravity (and sometimes other forces) to act on the object; that is, we can pretend that the object is a point with the same mass. The Center of Mass is identical to the Center of Gravity when you're working in a uniform gravitational field. The difference is irrelevant for racing. So for our purposes we will call them all Center of Gravity (CG).

To find the center of gravity for a system of particles, we can find the moments of the particles about a point. This is essentially the same thing as torque. Think of holding a bowling ball in your hand and at the end of a (strong) stick. There is more torque when we put that heavy weight further away from the point at which you are holding it. If you had three identical masses at the end of identical rods, then you can see how you might want to configure them so that you could hold all three equally balanced. What if we had two masses, one of which was twice as much as the other mass? How would you want to “balance” these two masses?  Wouldn’t you want the lighter mass twice as far away from the balance point as the heavier mass?

In this way we can define the Center of Gravity, CG, of a system of masses, m_i, at different positions, r_i, as the weighted average of their locations:

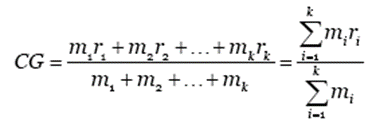
· The center of mass of a two-particle system lies on the line connecting the particles. The CG is closer to the more massive object.

· The CG of a ring is at the center of the ring (in the air).

· The CG of a solid triangle lies on all three medians and therefore at the centroid, which is also the average of the three vertices.

· The CG of a rectangle is at the intersection of the two diagonals.

· More generally, for any symmetry of a body, its center of mass will be a fixed point of that symmetry.

For physical objects — like cars — the center of gravity may not (and probably will not) be at the same place as the geometric center of gravity.

Why do we care about the Center of Gravity in racing? The higher a car’s center of gravity, the easier it is for outside forces to move it laterally on the track. We have heard of the SUV Rollover effect, where the high center of gravity in conjunction with a narrow wheelbase makes it much easier for an SUV to rollover in an accident. You will note that you don’t usually see a lot of accidents where a Mazda Miata or another small sports car has rolled (unless extremely high speeds or driver stupidity is involved). Why not? We do often hear about large trucks that roll and lose their loads — often as their loads shift in a turn. (Why is this?)

The ideal race car would have a CG as low as possible — hopefully just bare inches above the track. This would help it hold to the track as it speeds around the curves and would help to keep any lifting forces from moving the car up, thus losing traction.

Driving stock cars depends on a number of factors. Without an appropriately balanced center of gravity, the car will not able to move smoothly around a racetrack. The following diagram displays this concept (diagram and formulas courtesy of Emmons, 1992):

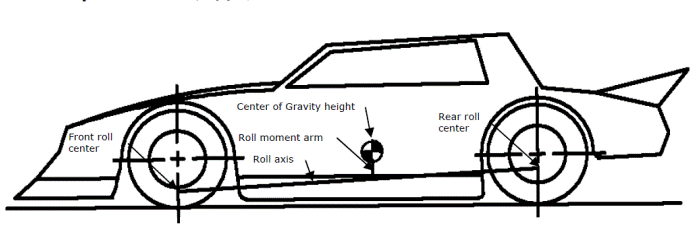
The roll axis is the theoretical line, which connects the front roll center to the rear roll center. The roll centers are the points along the axes where the car pivots left and right and up and down when it corners. The roll axis is the line about which the car rolls when you turn. One would hope that for the most part these roll centers are close to the middle of the front and rear axes. If not, then the car will be sliding one way or another as the weight shifts unequally about the roll axis.

Now the cornering forces affect the car at its center of gravity (CG). The distance between the roll axis and the center of gravity is called the Roll Moment Arm. This distance is what determines how much weight is transferred in cornering.

The Roll Moment Arm (MA) can be computed using the following formula:

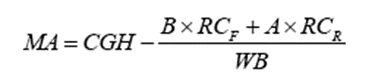
where CGH is the center of gravity height, WB is the wheelbase (distance between front and rear axles), RC_F is the front roll center height and RC_R is the rear roll center height (shown in the diagram).

Car engineers do not distribute the weight of the cars evenly between the front and rear axles, they have found if more weight is in the rear of the car, then the car handles better on the track. They have found the optimal percentage of weight transfer is 52% of the weight in the rear and 48% of the weight in the front. In the Moment Arm formula above, A represents the wheelbase times the rear weight percentage and B represents the wheelbase times the front weight percentage.

1. Find A and B.
2. All NASCAR cars have a wheelbase of 110 inches. If the front roll center height is 2.5 inches, the rear roll center height is 11 inches, and the center of gravity height is 15, find the length of the moment arm for the car.
3. Find the angle of depression from the line parallel to the ground that intersects the center of the front wheel to the bottom of the moment arm. HINT: the wheelbase is 110 inches and the center of gravity is not in the center since 52% of the weight is in the back of the car and 42% of the weight is in the front of the car.
4. Now we’re going to do the same for the back of the car. Find the angle of depression from the line parallel to the ground that intersects the center of the rear wheel to the bottom of the moment arm.

To build a car that will “stick” to the track and not move or sway too much in the turns, the engineers have to consider several items. There is the downward force of the air moving over the car that pushes the car down onto the track. There is the upward lift of the air that runs under the car that wants to push it up off of the track. These are controlled by the air foil and the general shape of the car for the downward force and the air-dam in the front of the car for the lifting force. Other items to be considered are the friction of the tires on the track (too keep it from sliding around the turns) and the height of the center of gravity of the car above the track.  If the CG is close to the track it will take a lot more force to cause it to roll over or to get lifted into the air — where it acts like a huge airplane wing and the driver gets airborne and terrible things begin to happen.

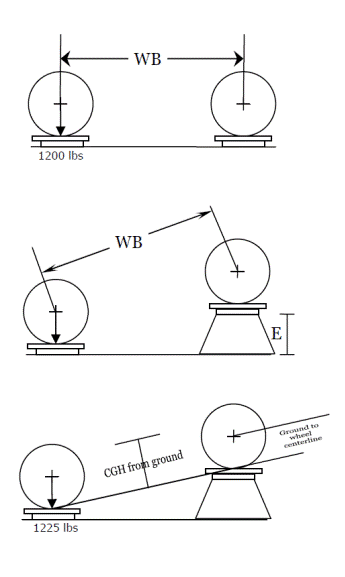How do the engineers determine the CGH (center of gravity height)? They actually weigh the car in a known configuration using four scales — one under each tire. We will assume that the car weighs 2500 pounds. Since the weight is distributed with 48% in the front of the car, the front scales should read 1200 pounds when the car is level.  Now, raise the rear end of the car a certain height, E. The weight of the car will be redistributed and we will find that the front tires now carry a weight of 1225 pounds. This has to be determined empirically! From there we can start our computations. First, we need to find the angle at which we have raised the rear end. Since E is the opposite side and the wheelbase, WB, is the hypotenuse, we get that

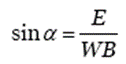
For example, if you raised the car with the wheelbase of 110″ up to a height of 24″, then

sin a =  = 0.2181818 and a = 12.602°

Now to compute the height of the CG above the roll axis — the center line joining the front and rear tires — we have to compute a few “moments”. It all works through the following formula:

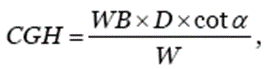
where D = angled front weight minus the level front weight and W is the total car weight. Now, to compute the height above the ground, we will have to add this distance to the height of the center line of the wheels to the ground.

In our example then, we have:

WB = 110, D = 1225 — 1200, W = 2500, and a = 12.602°.  Thus,

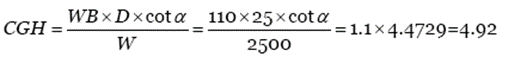
and the height of the center of gravity above the roll axis is 4.92 inches. If the ground to center line of the wheels is 12.75 inches, then the center of gravity is 17.67 inches above the ground. Compare that to the center of gravity height of an SUV, which will be in the 30 inch range.

5. Find the center of gravity height of the following car. The wheelbase is 109 inches, level front weight is 1230 pounds, the angled front weight is 1310 pounds, the amount you elevated the rear is 27 inches, and the total weight is 2500 pounds. Assume that you have 12 ¼ inches from the ground to the centerline of the wheels.

Calculating Tire Dimensions

1. 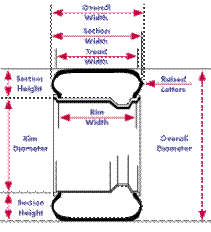Section Height = Width × Aspect Ratio

2. Combined Section Height = 2 × Section Height

3. Tire Diameter = Combined Section Height + Wheel Diameter

Example: 185/60R14 85H or 185/60HR14

SH = 185mm × .60=111mm

CSH = 111mm × 2=222mm

Diameter = 222mm + 355.6mm = 577.6mm = 22.74″

* The first number (185) is the width of the tire in millimeters, measured from sidewall to sidewall. To convert to inches, divide by 25.4. In our example the width is 185mm or 7.28″.

* The second number(60) is the aspect ratio. This is a ratio of sidewall height to width. In our example the tire is 7.28″ wide, multiply that by the aspect ratio to find the height of one sidewall. In this case, 185 × 0.60 = 111 mm or 7.28″× 0.60=4.37″.

* The last number is the diameter of the wheel in inches. To figure the outside diameter of a tire, take the sidewall height and multiply by 2,(remember that the diameter is made up of 2 sidewalls, the one above the wheel, and the one below the wheel) and add the diameter of the wheel to get your answer.  In our example the TIRE diameter will be 2 × 4.37 + 14 = 22.74″.

6. A 2008 Ford F-350 Standard Cab uses size 275/65HR20 tires. What is the outside diameter of each tire?
7. What is the centerline height of the tires for this F-350?
8. This truck has the following dimensions:

Wheelbase: ............. 158 inches

Length: .................... 243.2 inches

Width: ..................... 79.9 inches

Weight: .................... 5,300 pounds

Center of Gravity:... 22.4″

Assume that the truck carries 55% of its weight forward on level ground. If they raised the rear of the truck by 24″, how much of the weight was forward when it was on the incline.

9. Get online and see how much of the information you can find about your car. Also, compare the Mini Cooper, a Mazda Miata and the Hummer.