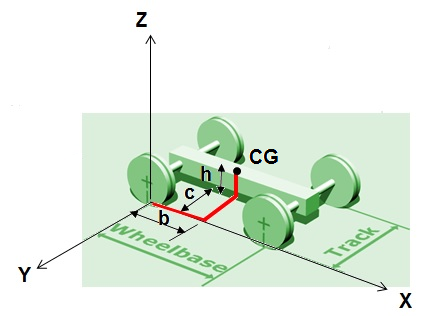
Step by step to find the car center of gravity/ mass (CG/ CM)

The center of gravity definition. The point in any solid where a single applied force could support it; the point where the mass of the object is equally balanced. The center of gravity is also called the center of mass.

So, to find this point means you have to get its distances form an arbitrary point in the three dimensions (X, Y, and Z).

To get the CG for your go kart you will need the following

A) To find the CG in the X and Y directions

Assuming it has a light weight:

You will need this:

- 4 measuring weight scale (which are using in most homes to measure man/woman weight), they should be in the same height range (for accuracy).

- A measuring tape

* You can use either of the SI units, or the imperial, the US customary units of measurement.

Steps:

- Put each Kart wheel on one of the weight scales.

- Be sure that the reading of each weight scale is not out of range (if so, or you need more chipper less accurate method,  see this other method to obtain each of the wheel weight “http://thecartech.com/AutoScience/Videos/car_weight.aspx”)

- Find the weight (weight “W” = reaction “R”) of each wheel- weight measurements.

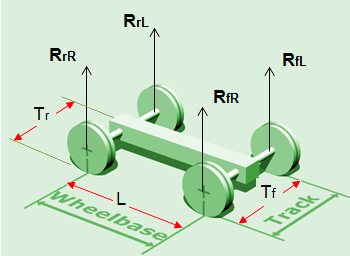
- Measure the lengths of (wheel base “L”, front track “T_f”, rear track “T_r”)- length measurements.

W = R	Rear wheel Right (RrR)	Rear wheel Lift (RrL)	Front wheel Right (RfR)	Front wheel Lift (RfL)
Wheel weight
	Rear Track (Tr)	Wheel base (L)	Front Track (Tf)
Distance

* You can use either of the SI units (kg, mm), or the imperial, the US customary units of measurement (lb, in).

** The measurements of the Track is from each wheel center line on one side  to the other wheel center line on the other side.

Equation variables:

	Kg or lb
Rear axle weight/reaction (Rr = RrR + RrL)
Front axle weight/reaction (Rf = RfR + RfL)
Lift side weight/reaction (RL = RrL + RfL)
Right side weight/reaction (RR = RrR + RfR)
Total car weight (W = RrR + RrL + RfR + RfL)

	mm or in
The deference between the front- and rear- tracks (f = Tr  - Tf)

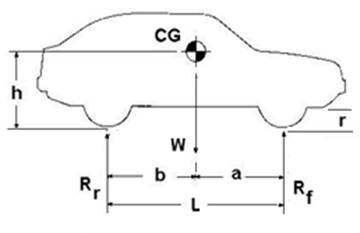
1- Finding the CG point location in the X-direction:

- Measure the distance between the points of contact of the wheels in the X-direction (the front axle and the rear axle), the distance L “the wheel base”, Now your point of reference is the contact point (between tire and ground) of the kart right wheel.

- Use the balancing equation to find CG point location in X-direction:

S M _A = 0

* where point A is a point of in the middle of the tire patch area of the rear left wheel.

R_f . L = W . b

b = (R_f/W) . L ------------------------------------------------(1)

2- Finding the CG point location in the Y-direction:

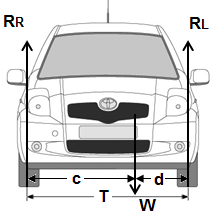
A- If the car has a symmetry (the engine in the middle, gearbox/transmission, …etc.) you don’t have to calculate. (assume c = T/2 “half the track”, approximately), if not, then:

SM_A = 0

W . c = R_L . T

c = (R_L/W) . T ………………………………………………(2)

B- Assuming the front and rear wheel track are the same/nearly the same (No symmetry):

- Measure the distance between the points of contact of the wheels in the Y-direction (the right and left side wheels), the distance T

C- Assuming the front and rear wheel track are NOT the same/nearly the same (NO symmetry):

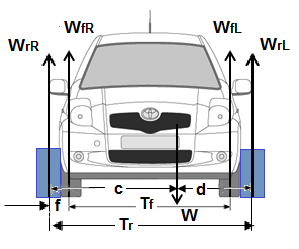
SM_A

W. c = W_rL . T_r + W_fL . T_f + W_fr . f

c = (W_rL . T_r + W_fL . T_f + W_fr . f)/W ………………………….(3)

To find the CG distance in the Z direction

- Raise the front of the kart, and place the front wheel on raise level (in two identical cubes, or above a curb)

B. The height above ground of CG (h):

The weight of the rear axle (W_r1) will be weighed while the front pair of wheels are raised up quite a small distance H.

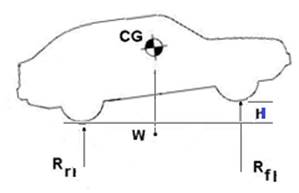
Then you can with the help of the link http://www.thecartech.com/subjects/auto_eng/Center_of_Gravity.htm (The height above ground of CG (h)) find the h distance of the CG above the ground.

* point A in this link at the center of the rear axle, (you need to measure the radius of the wheel too.)

B. The findings

	The CG location (mm or in)
The distance in the X direction (b)
The distance in the Y direction (c)
The distance in the Z direction (h)