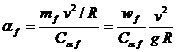HANDLING CHARACTERISTICS

OF ROAD VEHICLES

Handling characteristics of a road vehicle are concerned with its response to steering commands and to environmental inputs affecting the direction of motion of the vehicle such as wind and road disturbances. There are two basic problems in vehicle handling: one is the control of the vehicle to a desired path, the other is the stabilization of the direction of motion against external disturbances

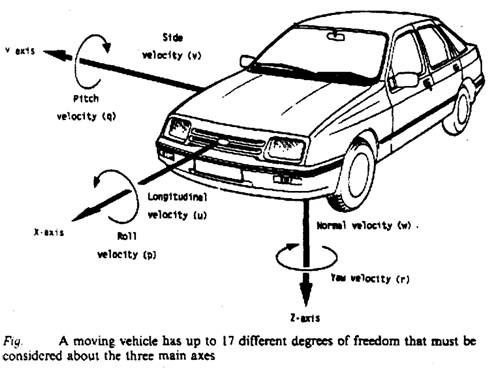
The vehicle as a rigid body has six degrees of freedom as shown in the figure. The motions associated with sideslip are:

1. motion along the y axis (side velocity, or lateral velocity, v_s or v_y),

2. rotation about the z axis (yaw velocity, Ω_z, and

3. rotation about the x axis (roll velocity) are usually referred to as lateral motions of the vehicle.

The behavior of the vehicle in these modes determines, to a great extent, its handling characteristics.

To study of vehicle handling, a simplified linear vehicle model in which the suspension is neglected will be examined. This model demonstrates the effects of tire properties, location of the center of gravity, and forward speed of the vehicle on the handling behavior.

Steering Geometry

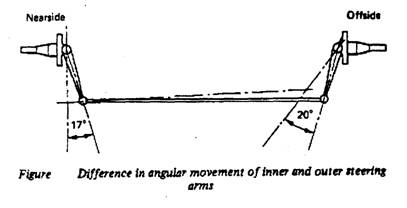
In examining the handling characteristics of a road vehicle, it is convenient to begin with the discussion of the cornering behavior of the vehicle at low speeds with the effect of the centrifugal force being read vehicles, steering is normally effected by changing the heading of the front wheels through the steering system. At low speeds, there is a simple relation between the direction of motion of the vehicle and the steering wheel angle, and the turning behavior mainly depends on the geometry of the steering linkage.

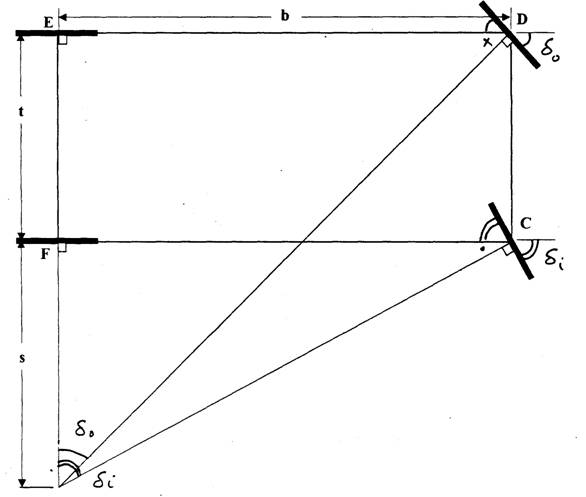
The prime consideration in the design of the steering system geometry is minimum tire scrub during cornering. This required that during the turn all tires should be in pure rolling without lateral sliding. To satisfy this requirement, the wheels should follow curved paths with radii originating from a common center as shown in the figure. This establishes the proper relationship between the steer angle of the inside front wheel δ_i and the outside front wheel δ_o.

From the figure it can be readily seen that angles d and d should satisfy the following relationship.

From D DEO

          cot δ_o = (t + s) / b

and from D DEO          

cot δ_i = s / b

Then

cot δ_o - cot δ_i = t / b                           (*)

where t and b the track and wheelbase of the vehicle respectively.

The steering geometry that satisfies equation (*) is usually referred to as the Ackerman steering geometry.

Ackerman steering geometry

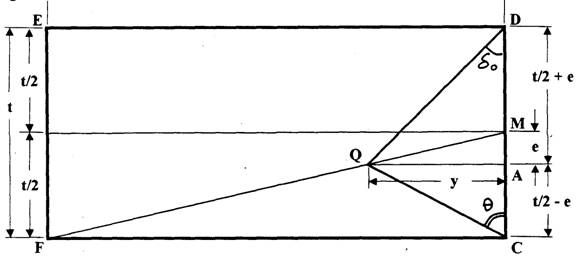
The relationship between δ_i and δ_o can be illustrated graphically as shown in the figure

                   cot δ_o = (t/2 + e) / y

and               cot θ = (t/2 - e) / y

then            cot δ_o - cot θ = 2 e / y

since triangle  D MAQ is similar to triangle D MCF

e / y = (t / 2) / b

then

cot δ_o -  cot θ = 2 e / y

cot δ_o -  cot θ = t / b

then form equation (*) and the above equation we can conclude (θ = δ_i)

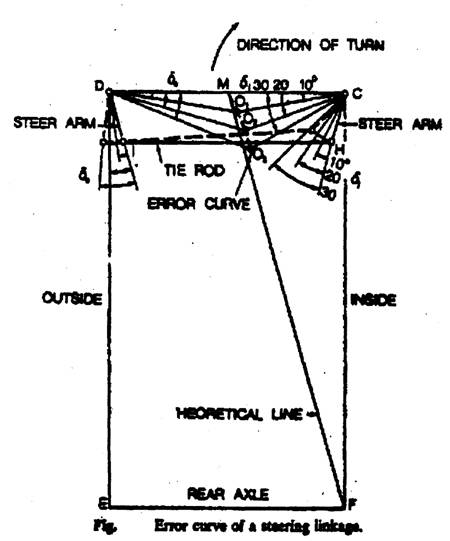
The results of the above analysis indicates that if the steer angles of the front wheels δ_i and δ_o satisfy equation (*), then by laying out the steer angle δ_i and δ_o from the front axle, the intersection of the non common sides of δ_i and δ_o will lie on the straight line connecting the midpoint of the front axle and the center of the inside rear wheel (i.e., line MF in the figure).

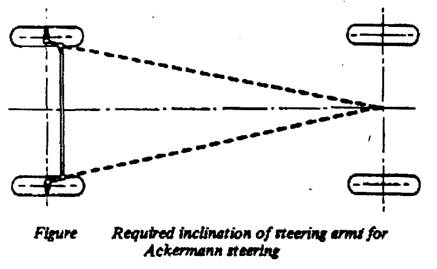
This geometry can be obtain by drawing lines through the steering arms to intersect on, or near, the axis of the rear axle, as shown in the above figure. This is arrangement is called Ackermann linkage.

Using a graphic method we may evaluate the characteristics of a particular steering linkage with respect to the Ackerman steering geometry, as shown in the figure.

The deviation of the curve connecting O₁, O₂, and O₃ from line MF is therefore an indication of the error of the steering geometry with respect to Ackerman criterion. Steering geometry deviates excessively form line MF will result in excessive tire wear and increased steering effort.

STEADY-STATE HANDLING CHARACTERISTICS

Steady-state handling performance is concerned with the directional behavior of a vehicle during a turn under non-time-varying conditions. An example of a steady-state turn is a vehicle negotiating a curve with constant radius at constant forward speed. In the analysis of steady-state handling behavior, the inertia properties of the vehicle are not involved.

When a vehicle is negotiating a turn at moderate or high, speeds, the effect of the centrifugal force acting at the center of gravity can no longer be neglected. To balance the centrifugal force the tires must develop appropriate cornering forces. A side force acting on a tire produces a side slip angle.

Slip angle α

Slip angle α is the angle formed between the direction of wheel travel and the line of intersection of the wheel plane with the road surface.

Tire cornering (lateral) stiffness C_α

The cornering stiffness C_α is used to compare the cornering behavior of different tires, which is defined as:

The handling characteristics of the vehicle depend, to a great extent, on the relationship between the slip angles of the front and rear tires, α_f and α_r.

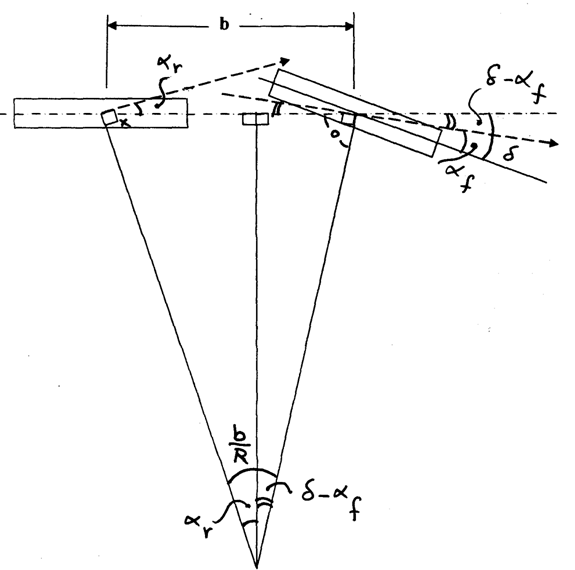
To simplify the analysis, the pair of tires on an axle is represented by a single tire with double the cornering stiffness as shown in the figure.

                                        (**)

where w is the total weight of vehicle, g is the acceleration due to gravity, v is vehicle forward speed, and other parameters are shown in the figure. The normal load on each of the front wheels w_f and that on each of the rear wheels w_r under static conditions. C_αf and C_αr are the cornering stiffness of each of the front and rear tires, respectively. K_us is usually referred to as the understeer coefficient, and is expressed in radians. Equation (**) is the fundamental equation governing the steady-state handling behavior of a road vehicle. It indicates that the steer angle required to negotiate a given curve depends on the wheelbase, weight distribution, forward speed and tire cornering stiffness.

The cornering stiffness of a given tire varies with a number of operational parameters including:

• inflation pressure,

• normal load,

• tractive (or braking) effort,

• and lateral force.

It may be regarded as a constant only within a limited range of operating conditions.

Dependent on the values of the understeer coefficient or the relationship between the slip angles of the front and rear tires, the steady-state handling characteristics may be classified into three categories:

• neutral steer,

• understeer and

• oversteer.

Neutral Steer

When the under steer coefficient K_us = 0, which is equivalent to the slip angles of the front and rear tires bring equal (i.e., α_f = α_r and w_f /C_αf = w_r/C_αr), the steer angle δ required to negotiate a given curve is independent of forward speed and is given by

                             δ = b / R

Understeer

When the understeer coefficient K_us > 0, which is equivalent to the slip angle of the front tire af being greater than that of the rear tire ar, (i.e., α_f > α_r and w_f /C_αf > w_r/C_αr),  the steer angle required to negotiate a given curve increases with the square of vehicle forward speed.

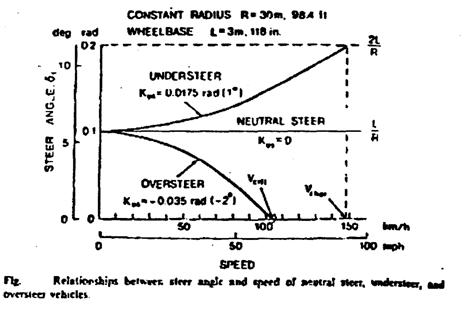
For an understeer vehicle, a characteristic speed v_char may be identified. It is the speed at which the steer angle required to negotiate a turn is equal to 2b/R, as shown in the figure. From equation (**)

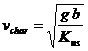
Oversteer

When the understeer coefficient K_us which is equivalent to the slip angle of the front tire α_f being less than that of the rear tire α_r (i.e., α_f < α_r, and w_f /C_αf < w_r /C_αr), the steer angle required to negotiate a given curve decreases with the increase of vehicle forward speed.

For all oversteer vehicle, a critical speed v_char, can be identified. It is the speed at which the steer angle required to negotiate any turn is zero as shown in figure below.

From Eq. (**)

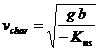
It should be noted that for an oversteer vehicle the understeer coefficient K_us, in the above equation has a negative sign. It will be shown later that the critical speed also represents the speed above which an over steer vehicle exhibits directional instability.

From the figure above one can conclude:

o The characteristics of neutral steer, for a constant radius turn are represented by a horizontal line in the steer angle-speed diagram shown in the figure.

o The characteristics of understeer, for a constant radius turn are represented by a parabola in the steer angle-speed diagram shown in the figure.

o The relationship of oversteer, between the required steer angle and forward speed for this kind of vehicle at a constant radius turn is illustrated in the figure.

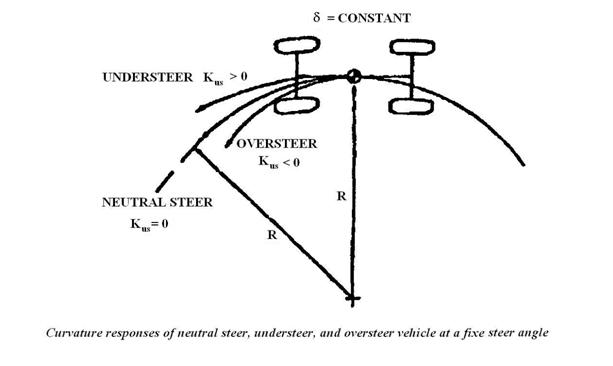
o For a neutral steer vehicle, when it is speeding in a constant radius turn, the driver should maintain the same steering wheel position. In other words, when a vehicle is speeding with the steering wheel fixed, the turning radius remains the same, as illustrated in the figure.

o For an understeer vehicle, when it is speeding in a constant radius turn, the driver must increase the steer angle. In other words, when it is accelerated with the steering wheel fixed, the turning radius increases, as illustrated in the figure.

o For an oversteer vehicle, when it is speeding in a constant radius turn, the driver must decrease the steer angle. In other words, when it is speeding with the steering wheel fixed, the turning radius decreases, as illustrated in the figure.

o When a neutral steer-vehicle moving on a straight course is subjected to a side force acting at the center of gravity, equal slip angles will he developed at the front and rear tires (i.e., α_f = α_r). As a result, the vehicle follows a straight line path at an angle to the original as shown in the figure.

o When a side force acts at the center of gravity of an understeer vehicle, the front tires will develop a slip angle greater than that of the rear tires (i.e., α_f > α_r) As a result, a yaw motion is initiated and the vehicle turns away from the side force as shown in the figure.

o When a side force acts at the center of gravity of an oversteer vehicle originally proceeding in a straight line, the front tires will develop a slip angle less than that of the rear tires (i.e., α_f < α_r). As a result a yaw motion is initiated, and the vehicle turns into the side force as illustrated in the figure.

The prime factors controlling the steady-state handling characteristics of a vehicle are the weight distribution of the vehicle and the cornering stiffness of the tires.

• A front-engined, front-wheel-drive vehicle with large proportion of the vehicle weight on the front tires may tend to exhibit understeer behavior.

• A rear-engine, rear-wheel-drive car with large proportion of the vehicle weight on the rear tires, on the other hand, may tend to have oversteer characteristics.

• Lowering the inflation pressure in the rear tires can have similar effects, as the cornering stiffness of a tire usually decreases with the decrease of inflation pressure.

• The application, of driving or braking torque to the tire during a turn will also affect the cornering behavior of the vehicle, as driving or braking torque modifies the cornering properties of the tire.

• Installing laterally stiff radial-ply tires on the front and relatively flexible bias ply tires on the rear may change an otherwise understeer vehicle to an oversteer one.

• The lateral load transfer from the inside tire to the outside tire on an axle during cornering will increase the slip angle required to generate a specific cornering force. Thus lateral load transfer will affect the handling behavior of the vehicle.

• For a rear-wheel-drive vehicle, the application of tractive effort during a turn reduces the cornering stiffness of the rear tires, producing an over steering effect.

• On the other hand, for a front-wheel-drive car, the application of tractive effort during a turn reduces the cornering stiffness of the front tires, thus introducing an under steering effect.

* Mixing of radial-ply with bias-ply tires in a vehicle may have serious consequences in its handling characteristics.

Among the three types of steady-state handling behavior, oversteer is not desirable from directional stability point of view. It is considered desirable for a road vehicle to have a small degree of understeer up to a certain level of lateral acceleration, such as 0.4 g.

Example

A passenger car has a weight of 20.105 kN and a wheel base of 3.2 m. The weight distribution on the front axle is 53.5% and that on the rear axle is 46.5% under static conditions.

A- If the cornering stiffness of each of the front tires is 38.92 kN/rad and that of the rear tires is 38.25 kN/rad, determine the steady-state handling behavior of the vehicle.

B- If the front tires are replaced by a pair of radial tires, each of which has a cornering stiffness of 47.82 kN/rad, and the rear tires remain unchanged, determine the steady- state handling behavior of the vehicle under these circumstances.

Solution:

A- The under steer coefficient of the vehicle is

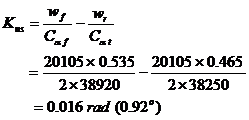
The vehicle is understeer and the characteristic speed is

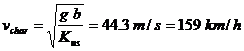
B- When a pair of radial tires with higher cornering stiffness is installed in the front axle, the understeer coefficient of the vehicle is

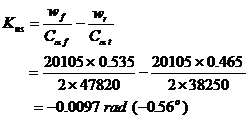
The vehicle is oversteer and the characteristic speed is

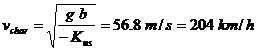
STEADY-STATE RESPONSE TO STEERING INPUT

Yaw Velocity Response

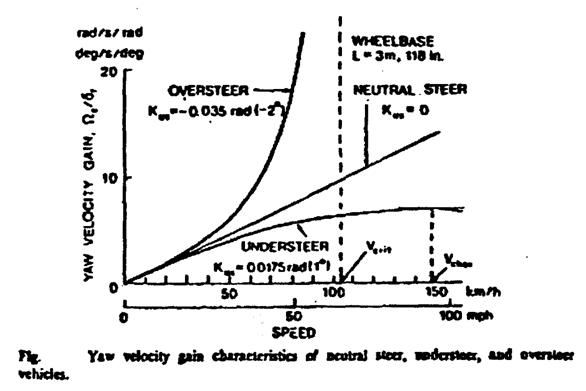
Yaw velocity gain is an often used parameter for comparing the steering response of road vehicles. It is defined as the ratio of the steady state yaw velocity to the steer angle. Yaw velocity Ω_z of the vehicle under steady state conditions is the ratio of the forward speed v to the turning radius R. From equation (**), the yaw velocity gain G_yaw

is given by

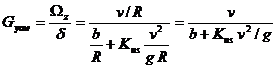
From the figure:  

• For neutral steer vehicle, the under steer coefficient K_us is zero, the yaw velocity gain increases linearly with the increase of forward speed.

• For an under steer vehicle, the understeer coefficient K_us is positive. The yaw velocity gain first increases with the increase of forward speed and reaches a maximum at a particular speed as shown in the figure (v_char)

• For an oversteer vehicle, the understeer coefficient K_us is negative, the yaw velocity gain increases with the forward speed at an increasing rate as shown. The yaw velocity gain approaches infinity at the critical speed v_char.