Homework 1:

1- A car has the following data:

- Net engine horsepower 100 kW at 6000 rpm (P_max, N_Pmax)

- Maximum torque 150 Nm at 3200 rpm (T_max, N_Tmax)

- Maximum speed 185 km/h (V_max)

- Curb weight 1160 kg (W_c = m_c g)

- Gross vehicle weight 1600 kg (W_g = m_g g)

- Transmission ratios 3.91/2.17/1.37/1.00 (ig₁/ig₂/g₃/g₄)

- Final drive ratio 3.46 (i_f)

- Wheel base 2666 mm (b = 2.666 m)

- Tire 185/65 R15 87H (w/ar RD” 87/H)

- Weight distribution front/rear 60/40 (R_f = 0.6W, R_r = 0.4W)

- CG height = 0.6 m (h)

 

Find:

     A)   Maximum gradient the car can climb S% or θ

B)   The weight distribution at that gradient R’_f, R’_r

C)   Maximum acceleration the car can achieve on direct drive at T_max. If:

-         Car coefficient of air resistance (drag coefficient) is 0.3 C_d

-         Air density 1.12 kg/m² ρ

-         Car fontal area 2 m² A_f

-         Rolling resistance coefficient 0.015 f_r

In case of:

i)                   curb weight, level road, no wind W_c, θ = 0, v_air= 0

ii)                 curb weight, level road, against wind of (18 km/h) W_c, θ = 0, v_air= 18

iii)               Gross vehicle weight, level road, no wind. W_g, θ = 0, v_air= 0

 

 

Solution:

A) TE = T_max ig₁ i_f  h_t / r_w

 

r_w = (2 h + D . 25.4)/2 = (2 (w . ar/100) + D . 2.54)/2

    = (2 x 185 x 65/100) +15 x 25.4)/2 = (240.4+ 381)/2

    = 310.7 mm = 0.31 m

 

assume h_t = 100%

TE = 150 x 3.91 x 3.46 x 1/ 0.3107 = 6531.35 N

RR = f_r W_g = 0.015 x 1600 x 9.81 = 235.44 N

SE = TE – RR = W sin θ = 6531.35 – 235.44 = 6295.91 N

sin θ = 6295.91/ (1600 x 9.81) = 0.4  or θ = 23.64^o

B)

 

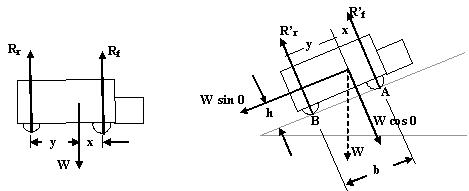
Since R_f / R_r = 60 /40  then x / y = 40 /60

 

x = 0.40 b , y = 0.60 b

 

 

S M_B = R^’_f  b – W cos θ  y + W sin θ  h = 0

 

R’_f  b = W cos θ  y -  W sin θ  h

 

R’_f = W (y/b) cos θ – W (h/b) sin θ  

      = W ( 0.6 cos 23.64 – (0.6/2.666) sin 23.64)

      = W ( 0.5496 – 0.090) = 0.4596 W = 0.4596 (1600 x 9.81) = 7213.88 N

 

R’_r = W – R’_f  = W – 0.4596 W

      = 0.5404 W = 0.5404 (1600 x 9.81) = 8482.12 N

 

 

C)

      v_car  at direct drive at T_max  (N_e = 3200 rpm)

v_car = (2 p r_w N_e / i_f ) (60/1000)  km/h

 

       = 0.377 N_e r_w / i_f   = 0.377 x 3200 x  0.31 / 3.46 = 108 km/h

 

AR = ½ ρ C_d A_f (v_car)² = ½ (1.12) (0.3) (2) (108/3.6)²

 

      = 302.4 N (no wind) case (i, iii)

 

AR = ½ ρ C_d A_f (v_car + 18)² = ½ (1.12) (0.3) (2) ((108 + 18)/3.6)²

 

AR = 411.6 N (head wind 18 km/h) case (ii)

 

RR = f_r W_c = 0.015 (1160) 9.81 = 170.7 N (curb weight) cas (i, ii)

 

RR = f_r W_g = 0.015 (1600) 9.81 = 235.4 N (GVW) case (iii)

 

TE = T_max x 1 x i_f / r_w = 150 (3.46) / 0.3107 = 1670.4 N case (i, ii, iii)

 

TR = AR + RR

 

SE = TE – TR

 

ma = SE

 

a = SE / m

 

m = 1160 kg case (i, ii)

m = 1600 kg case (iii)

 

i)

TR = AR + RR = 302.4 + 170.7= 473.1 N

 

SE = TE – TR = 1670.4 – 473.1 = 1197.3 N

 

a = SE / m = 1197.3/1160 = 1.032 m/s²

 

ii)

TR = AR + RR = 411.6 + 170.7 = 582.3 N

 

SE = TE – TR = 1670.4 – 582.3 = 1088.1 N

 

a = SE / m = 1088.1/1160 = 0.938 m/s²

 

iii)

TR = AR + RR = 302.4 + 235.4 = 537.8 N

 

SE = TE – TR = 1670.4 – 537.8 = 1132.6 N

 

a = SE / m = 1132.6 / 1600 = 0.708 m/s²