Axle shaft design

Axle Function:

The axle function is to transmit the engine torque to the wheel.

Loads on the axle:

1- Wheel torque (from engine):

Maximum limit for the wheel torque (due to engine torque) is:

Where:

                   (T_{w max})_engine = limit of wheel torque produce by the engine

T_{e max} = maximum engine torque (Nm)

                   i_g = gearbox ratio (maximum torque at 1^st gear ratio)

                   i_f  = final drive ratio

                   k_d = dynamic factor

                   k_l = the coefficient of differential locking (k_l = 0 for 4x2 cars with no differential locking)

Maximum limit for the wheel torque (due to road adhesion) is:

Where:

                   (T_{w max})_road = limit of road torque that can support wheel TE

f = coefficient of road adhesion

                   r_w = dynamic radius of the tire

                   R_w = vertical wheel reaction = ½ (W_r + wt)

          Where:

                             W_r = weight on the rear axle

                             wt = transferred weight

2- Wheel reaction R_w:

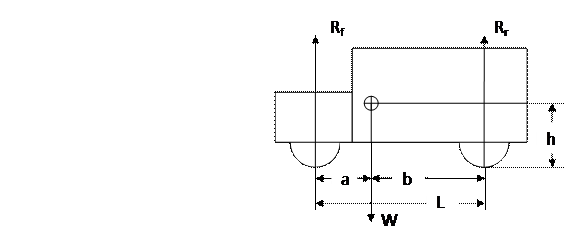
Where:

          W_r = static weight on the rear = rear weight ratio x W

                = (r.w.r x W) = (w_r/W) W

                = 45% W (for front engine RWD)

                = 40% W (for front engine FWD)

          Wt_a = transferred weight due to (acceleration- TE)

                 = ½ m x a x (h/L) = ½ W/g x  a x (h/L)

                 = ½ (TE_max – RR) (h/L)

        Limit of wt due to acceleration

wt_max = ½ f W (r.w.r)

  Wt_g = transferred weight due to (climbing a gradient)

                  = ½ w sin q (h/L) =  ½ (TE – RR) =  ½ (T_{e max} i_g i_f / r_w - RR)

The gradient limit:

W sin q = (W cos q b/L) f

tan q = (b/L) f ……… (slip)

W sin q  h = W cos q b

Tan q = b/h ………(turn over)

            wt_c = transferred weight due to (cornering)

                = W/g x (r.w.r) x w² R x (h/t)

The corner limit:

(roll over)

R_r = ½ (r.w.r) W

(skid)

wt_c = W (r.w.r) f (h/t)

Assumptions:

- The rear axle has no differential lock

- The car is a rigid body.

- Neglect car motion resistance

- The max transferred weight is:

(Normal force x coefficient of adhesion) x (dimension ratio)

- Limit of TE = Normal force x coefficient of adhesion

- Limit of F_b = Normal force x coefficient of adhesion

- Limit of F_c = Normal force x coefficient of adhesion

· Where normal force = static weight ± wt

· W_r = W (r.w.r)

Force in Z direction:

Case i (car moving with max acceleration):

* Limit of maximum acceleration: (ma = W (r.w.r) f)

(R_r)_i = W (r.w.r) + wt = W_r+ Wr f (h/L)

     = W_r (1 + f (h/L))

Case ii (car moving up a gradient):

(R_r)_ii = W_r cos q + wt = W_r  cos q + W sin q (h/L)

* Limit of maximum gradient (RWD):

TE = w sin q …… Engine torque

sin q = TE/ W  …… q = sin^-1 (TE/W) or

R_r f = [W  cos q (r.w.r) + W sin q (h/L)] f = W sin q ……. Wheel slip

W cos q (r.w.r) f = W sin q - W sin q (h/L) f = W sin q (1-  (h/L) f)

tan q = (r.w.r) f / (1-  (h/L) f)

q = tan^-1 [(r.w.r) f / (1-  (h/L) f)]

Overcome road irregularities (rear wheel dynamic reaction R_rd):

R_rd = R_r K_dr

Where

          k_dr = the dynamic factor of road:

                = 1.75 for cars, = 2.50 for trucks.

Case iii (Cornering):

(R_r)_{outer wheel} = (W_r + wt) = W_r + m v²/R  (h/t)

* skid limit
(R_r)_{outer wheel} = (W_r + wt) = ½ W_r + W (r.w.r) µ  (h/t)

* roll over limit

(R_r)_{outer wheel} = [(W (t/2) + (W/g  v²/R) h) / t] x (r.w.r)

Force in X direction:

Case i (max acceleration):

TE = T_{e max}  i_g i_f  k_d

Where:

          T_{e max} = maximum engine torque

          i_g = gear box ratio at 1^st gear

         i_f = final drive ratio

          k_d = dynamic factor (= 1.2-1.6)

* Limit of maximum TE: (TE = R_r f)

(TE_max)_i = (W_r + wt) f = (W_r + W_r (h/L) f) f = W_r (1 + (h/L) f) f

Case ii (max gradient):

(TE_max)_ii = W sin q  [q = sin^-1 (TE/W)] …….. Engine torque

or q = tan^-1 [(r.w.r) f / (1-  (h/L) f)] ……….wheel slip

TE h = W cos q  b …… (car turn over)

cos  q  = (TE/W) h/b …… q = cos^-1 (TE/W) h/b

Force in Y direction:

Case i (Cornering):

F_c = ½ mv²/R = ½ W (v²/R) (r.w.r)

* skid limit:

(F_c)_{out wheel} = ½ W (r.w.r) µ

* rollover limit:

m (v²/R) h =  W/g (v²/R) h = W t/2

 (F_c)_{out wheel} = W (r.w.r)/g (v²/R) = W (t/2h)