Design of disc clutches

Disc clutches can consist of single or multiple discs. Generally multiple disc clutches enable greater torque capacity but are harder to cool. Frictional clutches can be run dry or wet using oil. Typical coefficients are 0.07 for a wet clutch and 0.45 for a dry clutch.

Two basic assumptions are used in the development of procedures for disc clutch design based upon a uniform rate of wear at the mating surfaces or a uniform pressure distribution between the mating surfaces.

The assumption of a uniform pressure distribution at the interface between mating surfaces is valid for an unworn accurately manufactured clutch with rigid outer discs (new clutch).

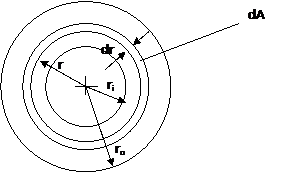The elemental axial force on an elemental annular ring is given by

The area of an elemental annular ring on a disc clutch, as shown in the figure:

Integrating to give the total axial force:

                                                                   ………………………..(1)

The friction torque “dT_c” that can be developed on an elemental ring is the product of the elemental normal force, given by “µ dF_n” and the radius “r”.

 dr

Where: µ is the coefficient of friction between the two mating surfaces.

The total torque is given by integration of the above equation between the limits of the annular ring, “r_i”, “r_o”:

                                                            …………………………(2)

The assumption of uniform pressure distribution:

Integrating equation (1) to get “F_n” where “p” is the assumed uniform pressure distribution, so

…………………………(3)

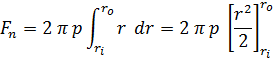Now that F_n is also the necessary force required to clamp the clutch discs together (F_n , normal force).

Integrating  equation (2) to get “T_c”.

Since “p” is a constant, then the integration becomes:

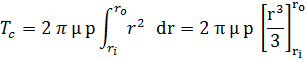
                                                         ……………………….. (4)

This equation represents the torque capacity of a clutch with a single frictional interface. In practice clutches use an even number of frictional surfaces.

For a clutch with n faces the torque capacity is given by:

                                              ………………………………(5)

Using equations (1), (3) and substituting for the pressure p, gives an equation for the torque capacity as a function of the axial clamping force.

                                                    ……………………………...(6)

Compare the above equation with:

We found in case of uniform pressure distribution the mean radius is:

                                                                   ………………………………(7)

The assumption of uniform wear:

The wear is assumed to be proportional to the product of the pressure and velocity. So

Where “ω” is the angular velocity (rad/s). For a constant angular velocity the maximum pressure will occur at the smallest radius.

Eliminating the angular velocity, the relationship for the pressure as a function of the radius is:

                                                                       ………………………….….(8)

 Integrating equation (1) to get “F_n”

                                                ……………………………..(9)

Rearranging the above equation gives

                                                            ……………………………..(10)

Substitute the value of “p” from equation (8) into equation (2) and integrate to get “T_c”

                                            …………………………….(11)

 Substituting “P_max” from equation (10) into equation (11) we get:

                                                                …………………………….(12)

For “n” friction surfaces (number of frictional plate x 2) the above equation becomes:

                                                           ……………………………..(13)

From the above equation the mean radius is:

                                                                         ……………………………..(14)

Comparing equations (5) and (11), one can find that the uniform wear has a lower torque capacity than the uniform pressure assumption. This is because the higher initial wear at the outer diameter shifts the center of pressure towards the inner radius.  

The previous equations indicate uniform wear assumption has a lower torque capacity than uniform pressure assumption. That can be seen in the above figure, when the clutch is new it has a higher torque capacity and there is a transient period till it comes to a uniform wear, where the torque capacity is lower.

Clutches are usually designed based on uniform wear. Since the uniform wear assumption gives a lower torque capacity clutch than the uniform pressure assumption. Designing the clutch using the uniform wear assumption to carry a maximum engine torque will need bigger disc clutch dimensions. The clutch bigger dimensions can carry the maximum engine torque when the clutch is old and when the clutch is new. Designing the clutch the other way around will lead to clutch slip when it becomes old.

Find the frictional clutch dimension using the uniform wear assumption:

As can be seen from equation (11)

The design calculation depends on:

- load value (T_c)

- material properties (µ, p_max)

- element or body dimensions (r_o, r_i)

Knowing the clutch torque capacity and the friction material properties, we still have two unknowns “r_o, r_i”. Now, we have one equation two unknowns. To solve this, let’s draw the value of “T_c “against “r_i” as fraction of “r_o”, as shown in the figure.

Or by differentiating equation (11) with respect to “r_i” and equating the result to zero.

The maximum torque for any outer radius “r_o” is found to occur when

To insure that the engine torque is fully transmitted under all working conditions without slip, a service factor is used to get the clutch torque capacity. 

Where:

            T_c is the clutch torque capacity

β is the service factor

            T_{e max} is the engine maximum torque

Table 1 gives an indication of the typical values for service factors.

Description of general system	Typical driven system	Type of drive
		Small electric motors, turbine	IC engines 4-6 cylinders	IC engines 2-3 cylinders	Single cylinder engine
Steady power source, steady load, no shock or overload	Belt drive, small generators, centrifugal pumps, fans machine tools	1.5	1.7	1.9	2.2
Steady power source, with some irregularity of load up to 1.5 times normal power	Light machinery for wood, metal and textiles, conveyor belts	1.8	2.0	2.4	2.7
	Large conveyor belts, larger machines reciprocating pumps	2.0	2.2	2.4	2.7
Frequent start-stops, overloads, cycling high inertia starts, high power, pulsating power source	Presses, punches, piston pumps, cranes, hoists	2.5	2.7	2.9	3.2
	Stone crushers, roll mils, heavy mixers, single cylinder compressors	3.0	3.2	3.4	3.7

Table 2 lists typical values for the properties of friction linings, dynamic friction coefficients, permissible contact pressure and temperature limits.

Material	µdry	µoil	pmax (MPa)	t (^oC)
Molded components	0.25 – 0.45	0.06 -0.10	1.035 -2.07	200 - 260
Woven materials	0.25 – 0.45	0.08 -0.10	0.345 - 0.69	200 - 260
Sintered metal	0.15 – 0.45	0.05 -0.08	1.035 -2.07	230 - 680
Cork	0.30 – 0.50	0.15 -0.25	0.055 - 0.1	80
Wood	0.20 – 0.45	0.12 -0.16	0.345 - 0.62	90
Cast iron	0.15 – 0.25	0.03 -0.06	0.69 -1.725	260
Paper based	-	0.10 -0.17
Graphite/resin	-	0.10 -0.14