Calculations and Science
Mass
In physics, mass is a property of a
physical body which determines the strength of its mutual gravitational
attraction to other bodies, its resistance to being accelerated by a force, and
in the theory of relativity gives the mass–energy content of a system. The SI
unit of mass is the kilogram (kg) and represented by the symbol m.
For everyday objects and energies
well-described by Newtonian physics, mass describes the amount of matter in an
object.
Weight
In science and engineering, the weight of
an object is usually taken to be the force on the object due to gravity. Weight
is a vector whose magnitude (a scalar quantity), often denoted by an italic
letter W, is the product of the mass m of the object and the magnitude of the
local gravitational acceleration g; thus: W = mg. The unit of measurement for
weight is that of force, which in the International System of Units (SI) is the newton.
Force
In physics, a force is any interaction
that, when unopposed, will change the motion of an object. In other words, a
force can cause an object with mass to change its velocity (which includes to
begin moving from a state of rest), i.e., to accelerate. Force can also be
described by intuitive concepts such as a push or a pull. A force has both
magnitude and direction, making it a vector quantity. It is measured in the SI
unit of newtons and represented by the symbol F.
Work
Work is done when a force overcomes resistance and causes movement. Work is measured by the product of the force and the distance moved in the direction of the force, the unit being the joule (J):
W = F s
Where:
W = work done in joules (J),
F= force in Newton (N), and
s = distance in meters (m) moved in the direction of the force.
If the force causes no movement, then no
work is done.
Energy
In physics, energy is a property of objects which can be transferred to other objects or converted into different forms, but cannot be created or destroyed. The "ability of a system to perform work" is a common description. For instance, in SI units, energy is measured in joules, and one joule is defined "mechanically", being the energy transferred to an object by the mechanical work of moving it a distance of 1 metre against a force of 1 newton. However, there are many other definitions of energy, depending on the context, such as thermal energy, radiant energy, electromagnetic, nuclear, etc., where definitions are derived that are the most convenient.
Common energy forms include the kinetic energy of a moving object, the radiant energy carried by light, the potential energy stored by an object's position in a force field (gravitational, electric or magnetic), elastic energy stored by stretching solid objects, chemical energy released when a fuel burns, and the thermal energy due to an object's temperature. All of the many forms of energy are convertible to other kinds of energy, and obey the law of conservation of energy which says that energy can be neither created nor be destroyed; however, it can change from one form to another.
Power
Power is the rate of doing work. The unit, the watt, is a rate of working of 1 joule per second (1 J/s)
power = work done per second
= Newton x meter per second
= Joule per second
= Watt
Torque
When a force acts on a body pivoted on a fixed axis, the product of the force perpendicular to the radius, and the radius at which it acts, is termed the turning moment of the force or torque. Torque is measured in Newton meters (N m) (to distinguish it from work). From the Figure:
|
where F= force in Newton (N), r = radius in meters (m), and T = torque in Newton meters (N m). |
|
Work done by torque
The work done by the torque per revolution is the product of the force and the distance moved in the direction of the force - that is, the circumference:
W = F x 2p r
= 2 p F r
where
W = work done in Joule (J),
F = force in Newton (N), and
r = radius in meters (m) at which the force acts.
The work done in n revolutions will be:
W = 2 p F r n Joule
If n revolutions are made per second (N/60), then the work done per second is
2 p F r Joule. This is the power produced:
P = 2p F r N/60
or
P = 2 p T N/60
P = w T
where
P = power in watts (W),
F r or
T = torque in Newton meter (N m),
N = rotational speed
(rev/min), and
w = angular speed (rad/sec).
Using these formulae, the power can be calculated from the torque and speed of a shaft.
Mean piston speed
The product of twice the stroke, measured in meters, and the rotational speed (rev/s) of the engine gives the mean or average piston speed in m/s.
v = 2 L N/60
where:
v = mean piston speed (m/s)
L = piston stroke (m)
N = engine rotation speed (rev/min), at each revolution the piston makes two strokes.
The higher the mean piston speed, the greater are the inertia forces of the reciprocating parts. The maximum mean piston speed usually employed with current production engines is about 16 m/s.
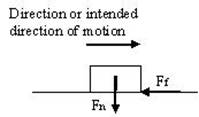
Friction force
It is found that the horizontal force required to drag a body over a smooth, level, dry surface is approximately a constant fraction of the perpendicular force between the surfaces. In Figure, W is the load or normal force Fn between the surfaces, and Ff is the force parallel to the surfaces or the friction force.
The ratio Ff / Fn , fairly constant for any given combination of two materials, is termed the coefficient of friction m.. The value of m depends upon the materials and the condition of the surfaces and not greatly upon the speed or area of contact.
|
|
In some cases - brakes, drive belts, clutch, tires - a high coefficient of
friction is required, whilst in others, such as bearings, a low coefficient is
necessary.
The friction force reaches a maximum value just before sliding occurs; this is static friction or stiction. It then reduces to a lower dynamic or kinetic value during sliding. The difference between these two values can have important results, e.g. during a cornering 'breakaway' when the centrifugal force exceeds the limit of the static friction force.
The coefficient of friction between the tires and the road may be almost zero under icy conditions. Alternatively, some braking distances indicate a coefficient exceeding 1.0, i.e. the frictional force is greater than the weight of the vehicle. Some interlocking between the tires and the road takes place where tread rubber is torn away.
When surfaces are separated by a film of lubricant, fluid friction rather than dry friction is involved. This viscous friction is related to the area of contact, the speed and the viscosity of the lubricant.
Table 1: Materials coefficients of static friction
|
Materials |
Coefficient of static friction |
|
Leather on cast iron |
0.4- 0.6 |
|
Friction material on cast iron |
0.35- 0.45 |
|
Cast iron on cast iron |
0.2- 0.3 |
|
Smooth greased wooden 'skids' |
0.05- 0.08 |
|
Plain bearing fluid friction |
0.02- 0.04 |
|
Ball bearing |
0.00- 0.004 |
Density
Density is the mass of a substance per unit volume (kg/m3). The density of water is, for practical purposes, 1000 kg/m3 or 1 kg/l. (The litre (l) is 10-3 m3.)
Relative density or specific gravity
The ratio (mass of a substance / mass of an equal volume of water)
is called the relative density of the substance, and represents how many times it is heavier or lighter than the same volume of water (Table 2). Note that relative density has no units.
Table 2: Substances relative densities
|
Substance |
Relative density |
|
Oxygen |
0.0014 |
|
Cork |
0.22 |
|
Paraffin/ petrol |
0.7/ 0.8 |
|
Water |
1.0 |
|
Magnesium |
1.7 |
|
Carbon |
2.0 |
|
Glass |
2.6 |
|
Aluminium |
2.7 |
|
Chromium |
6.6 |
|
Tin |
7.3 |
|
Iron/ steel |
7.2/ 8.0 |
|
Copper |
8.3 |
|
Nickel |
8.9 |
|
Molybdenum |
10.0 |
|
Lead |
11.4 |
|
Mercury |
13.6 |
|
Platinum |
21.5 |
In many cases only approximate figures can be given.
Pressure
Pressure is the force per unit area; the unit is N/m2 or the Pascal (Pa). Larger practical units are kN/m2 (kPa) and MN/m2 (MPa). Note that
1 MN/m2 (MPa) = 1N/mm2
A pressure of 7 MPa means that each mm2 subject to the pressure has a force of 7 N acting on it, and the total force on the surface will be the product of the pressure and the area:
|
pressure = force/ area force = pressure x area |
|
Atmospheric pressure
Air has weight. The atmosphere above the earth produces a pressure at sea level of approximately 1 bar, where 1 bar = 105 N/m2 or 105 Pa. Standard atmospheric pressure is 1.01325 bar, 1013.25 millibar or 101.325 kPa. Above sea level the atmospheric pressure will be less than 1 bar.
Gauge and absolute pressure
The ordinary pressure gauge gives readings measured above atmospheric pressure. To obtain the absolute pressure, that is the pressure measured above a perfect vacuum, atmospheric pressure must be added to the gauge reading:
absolute pressure = gauge pressure + atmospheric pressure
Stress
Components may be subject to a tensile load, as in a brake cable; a compressive load, as in a push rod; or a shear load, as in a shackle pin. In each case the value of the stress produced is found by dividing the load by the cross-sectional area on which it acts. Typical units of stress are N/m2 (Pa), kN/m2 (kPa) and MN/m2 (MPa).
F or tensile and compressive stress the cross-sectional area is measured at right angles to the direction of the force, while for shear stress the area is measured parallel to the direction of the force.
Temperature
The temperature, or degree of 'hotness' of a body, can be measured on the degree Celsius (oC) or the Kelvin (K) scale. The upper 'fixed' point -that is, the boiling point of water at atmospheric pressure - is 100 oC or 373.15 K, and the lower fixed point, the freezing point of water, is O oC or 273 K.
The melting points of various substances are shown in the next Table.
Table 3: Substances melting points
|
Substance |
Melting point (oC) |
|
Oxygen |
-219 |
|
Mercury |
-39 |
|
Tin |
232 |
|
Lead |
327 |
|
Zinc |
419 |
|
Magnesium |
633 |
|
Aluminium |
658 |
|
Brass |
900 |
|
Copper |
1083 |
|
Glass |
1100 |
|
Iron (cast) |
1200 |
|
Iron (wrought) |
1530 |
|
Nickel |
1452 |
|
Chromium |
1520 |
|
Platinum |
1755 |
|
Molybdenum |
2450 |
|
Carbon |
3500 |
Thermodynamic scale of temperature
At constant pressure the volume of a given mass of gas increases or decreases by (for practical purposes) 1/273 of its volume at 0 oC for each degree rise or fall. A theoretically 'perfect' gas would have no volume and no internal energy at -273oC.
The thermodynamic temperature scale uses -273o C as zero and temperature intervals in Kelvin, where 1 Kelvin exactly corresponds to 1 degree Celsius:
T = t + 273
Where
T = temperature in Kelvin (K) and
t = temperature in degrees Celsius (oC)
General gas law
When the temperature, or volume, or pressure of a given mass of gas changes, the relationship between them before and after the change is given by
(p1 V1 / T1) = (p2 V2 / T2)
where
p1 = initial absolute pressure
V1 = initial volume
T1 = initial thermodynamic temperature
p2 = final absolute pressure
V2 = final volume (in the same units as V1)
T2 = final thermodynamic temperature
Unit of heat
Heat is one of many forms of energy. It is stored in a substance in the kinetic (movement) energy of the molecules.
The unit of heat is the joule (J), which is also the unit of work. When mechanical energy is converted into heat energy the quantity of work done equals the quantity of heat produced, both measured in Joules. This relationship is known as the first law of thermodynamics.
In practice it is often convenient to measure heat in kilo Joules (kJ).
Specific heat capacity
The quantity of heat required to raise a mass of kg of a substance through 1 oC or 1 K is called the specific heat capacity of the substance. The units are joules per kilogram per degree Celsius (J/kg oC).
The specific heat capacities of various substances are shown in the Table. Approximate figures only can be given in some cases, since the specific heat capacity depends upon the composition of the substance and temperature range involved.
Table 4: Substances specific heat capacities
|
Substance |
Specific heat capacity (J/kg oC) |
|
Lead |
130 |
|
Mercury |
130 |
|
Tin |
225 |
|
Copper |
390 |
|
Iron |
500 |
|
Glass |
600 |
|
Aluminium |
900 |
|
Rubber |
1500 |
|
Petrol |
1800 |
|
Ice |
2100 |
|
Paraffin wax |
2900 |
|
Water |
4190 |
Quantity of heat
The quantity of heat required to raise a given mass of any substance through a given range of temperature can be calculated from
Q = mct
where
Q = quantity of heat (J),
m = mass of substance (kg),
c = specific heat capacity of substance (J/kgoC), and
t = rise in temperature (oC or K).
In a cooling process, t is the fall in temperature and Q is the quantity of heat lost by the body.
Specific latent heat
Heat is required to change a substance from the solid to the liquid state and from the liquid to the gaseous state. During a change of state the temperature remains constant at the melting or boiling point of the substance and the heat required is termed latent heat. During the reverse change of state, from gas to liquid or liquid to solid, latent heat is given out by the substance.
The heat required to change 1 kg of a substance from the solid to the liquid state is called the specific latent heat effusion of the substance, with units kJ/kg. Similarly the specific heat of vaporization is the heat needed to change 1 kg of the substance from the liquid state to vapour. At standard atmospheric pressure:
These quantities of heat required to change the state of the substance from ice to water or from water to steam without rise in temperature, may be compared with the sensible heat required to raise the temperature of water from O oC to 100 oC, which is 419 kJ/kg.
Transfer of heat
Heat may be transferred in three ways:
Conduction occurs when the heat energy passes from one particle of the substance to the next. Most metals are good conductors of heat; copper and aluminium are two of the best. Plastics, wood, cork and rubber are among the poor conductors of heat; they are employed as heat insulators. Liquids and gases are generally very poor conductors of heat.
Convection currents are produced in liquids and gases. One portion of the fluid is heated, expands and, becoming less dense, is displaced by the cooler and denser surrounding fluid.
Radiation is the transmission of heat energy from the surface of a body in the form of rays. A dull black surface will radiate and absorb heat more readily than a polished light surface.
Examples of the transfer of heat in the engine are the conduction of heat through the cylinder walls, setting up convection currents in the coolant; and the radiation of heat from the exhaust manifold surface.
The thermal conductivities of various substances are shown in the next Table.
Table 5: Substances thermal conductivities
|
Substance |
Thermal conductivity (W/m oC) |
|
Silver |
418.7 |
|
Copper |
382.3 |
|
Gold |
295.2 |
|
Aluminium |
203.5 |
|
Zinc |
110.1 |
|
Brass |
108.9 |
|
Iron (cast) |
75.37 |
|
Tin |
62.81 |
|
Lead |
34.75 |
|
Mercury |
7.955 |
|
Glass |
0.921 |
|
Carbon (graphite) |
0.628 |
|
Water |
0.590 |
|
Perspex |
0.209 |
|
Rubber |
0.188 |
|
Wood (oak) |
0.147 |
|
Cork |
0.050 |
|
Air |
0.024 |
Conversion of energy
Energy can be converted from one form to another, e.g.:
(a) Chemical energy into heat energy by combustion
(b) Heat energy into mechanical energy by a heat engine - one form being the internal
combustion engine
(c) Mechanical energy into electrical energy by a dynamo
(d) Electrical energy into mechanical energy by an electric motor
(e) Mechanical energy into heat energy by friction.
Coefficient of linear expansion
When a body expands, the fraction
[Increase In length produced by 1°C temperature rise / original length (same units as extension)]
is termed the coefficient of linear expansion per oC.
The coefficients of linear expansion for various substances are shown in the next table.
Table 6: Substances coefficients of linear expansion
|
Substance |
Coefficient of linear expansion per oC |
|
Invar( steelwith36% nickel) |
0.00000087 |
|
Glass/platinum |
0.000009 |
|
Iron |
0.000011 |
|
Nickel |
0.000013 |
|
Copper |
0.000017 |
|
Brass |
0.000019 |
|
Tin |
0.000022 |
|
Aluminium |
0.000023 |
|
Zinc |
0.000026 |
|
Lead |
0.000029 |
Examples:
Example 1
An iron block having a mass of 52 kg is cooled from 94°C by 8.5 litters of water at an initial temperature of 21°C. Calculate the rise in temperature of the water and the fall in the temperature of the block during the cooling process.
The specific heat capacity (SHC) of water is 4190 J/kgOC and of iron is 500 J/kg"C. Assuming no heat escapes during the exchange of heat:
quantity of heat lost by the iron block = quantity of heat gained by the water
mass of block x SHC iron x fall in temperature = mass of water x SHC water x rise temperature
Let the final temperature of the block and of the water be t oC. Then fall in temperature of block = (94 - t) oC
rise in temperature of water = (t - 21) oC
Therefore
52 x 500 x (94 - t) = 8.5 x 4190 x (t - 21)
2444000 – 26 000 t = 35 615 t - 747 915
61615 t = 3191915
t =51.8 oC
rise in temperature of water = 51.8 - 21 = 30.8 °C
fall in temperature of block = 94 - 51.8 = 42.2 °C
Example 2
A cylinder has a compression ratio of 8.4 to 1. At the commencement of the compression stroke it is filled with gas at a pressure of 96 kPa absolute and a temperature of 35 oC. What should be the pressure of gas, by gauge, at the end of the compression stroke if the temperature rises to 110 °C?
(Take atmospheric pressure = 101 kPa.)
where:
p1 = initial absolute pressure = 96 kPa absolute
V1 = initial volume = 8.4 unit
T1 = initial thermodynamic temperature = 35 + 273 = 308 K
P2 = final absolute pressure (required)
V2 = final volume = 1 unit
T2 = final thermodynamic temperature = 110 + 273 = 383 K
Hence
P2 = (p1 V1 / T1) . (T2 / V2)
= 96 x 8.4 x 383 / (308 x 1)
= 1002.8 kPa (absolute)
= (1002.8 – 101) kPa (gauge pressure)
= 901.8 kPa (gauge pressure)