Compression Spring Natural Frequency

Resonance is an issue for springs used in a dynamic cyclic loading environment, where the compressive force varies between two values. For example, the valve springs used in a car engine are subject to dynamic loads.

By design intent, a spring is a static mechanism. However, a spring will no longer behave as a static mechanism if the frequency of operation approaches the spring's first resonant frequency. Worse, the force the spring exerts on its boundaries will tend to decrease, which could have disastrous implications for the spring assembly.

In light of this, a rule of thumb for spring design is to make sure the frequency of operation is 15 to 20 times less than the first resonant frequency of the spring in question.

Use this calculator to find the first resonant frequency of a compression spring when you know its spring constant and its mass. (The spring mass can be found by weighing the spring.)

The frequency of the lowest spring resonance (in Hz) is found from the equation,

where k is the spring constant and M is the spring mass. The spring mass M can be found by weighing the spring.

If you do not know the mass of the spring, you can calculate it by multiplying the density of the spring material times the volume of the spring. Inserting this product into the above equation for the resonant frequency gives,

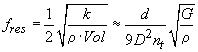
Expressed in Terms of Spring Geometry

We can express the natural frequency for the spring in terms of its geometry and shear modulus (instead of its overall stiffness k and its mass).

To do so, we find the volume of the spring,

and note the stiffness of the spring in terms of its geometry and shear modulus G and number of active coils n_a,

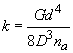
Substituting these two equations into the formula for f_res gives,

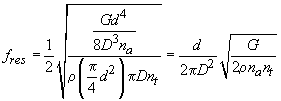
If the spring has several coils, we can assume that the number of active coils equals the number of total coils. We can also allow the following numerical approximation,

These two approximations give us our final equation for the spring resonant frequency,

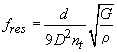
To use this formula we need to know the material's G and all of the spring geometry. It's much easier to use the formula from the last section which only needs the spring stiffness and mass, especially when working with springs where the material is uncertain.

G = 76.9- 81.4 GPa, ρ_steel  = 7500- 7800 kg/m³