Exercise 1:

1- Define the following

a- Stress, σ

b- Strain, ε

c- Modulus of Elasticity (Young’s Modulus), E

d- Modulus of Rigidity (Shear Modulus), G

e- Second Moment of Area, I

f- Polar Moment of Area, J

g- Bending moment Diagram, BMD

h- Torque, T

i- Moment, M

j- Friction force, F_f

k- Centroid of area

l- Factor of safety (Safety factor), SF

m- Example of:

i. Energy transmission elements

ii. Energy storage elements

iii. Locating (fixing, joining) elements

iv. Friction reduction elements

n- The differences between:

i.  Tensile and Compression Stresses, σ_t – σ_c

ii. Shear and Torsional Stresses, τ_s – τ_t

iii. Yield and Ultimate Stresses, σ_y – σ_u

iv. (Pa) and (MPa)

v. Simple beam and Cantilever

o- Find the following:

i. Area (A) and Second moment of area (I) of a rectangle (B,H)

ii. Area (A) and Second/Polar moment of area (I, J) of a circle (R)

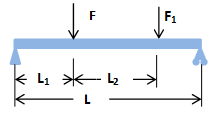
2- Find the point and value of maximum stress on the beam, (circular cross sectional area (d = 20 mm)) . Where: F = 150 N, F1 = 100 N, I = 2000 mm^4 L = 400 mm, L1 = 100 mm, L2 = 250 mm
Solution Hint: Using ΣFy = 0, ΣMo = 0, to find R1 = R2 = Draw: BMD and obtain point and value of Mmax Calculate: σb (using: M, y, I)

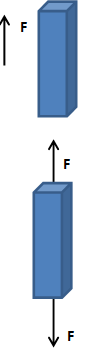
3- A Force of 2000 N, is applied on a tip of a beam of rectangular cross section (10 x 4 mm) and with a length of 120 mm. Chose suitable steel, taking SF = 6.

a- show the force direction on the element and the reaction due to this force to induce the following stress:

i- Tensile ii- Compression iii- Bending iv- Torsion, J = b h/[3 (b^2 + h^2)] v- Shear And find the stress due to the force applied: Solution; i- Tensile stress, σt = F/A = 2000/(10x4) = 50 MPa σt = σall =50 MPa σu = σall x SF = 50 x 6 = 300 MPa From chart 9, chose steel EN1A (420 MPa)