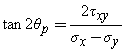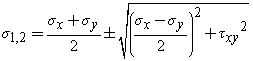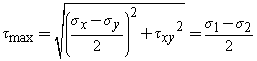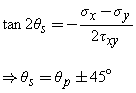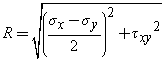Principal stresses

Given the stress components s_x, s_y, and t_xy, this calculator computes the principal stresses s₁, s₂, the principal angle q_p, the maximum shear stress t_max and its angle q_s. It also draws an approximate Mohr's circle for the given stress state.

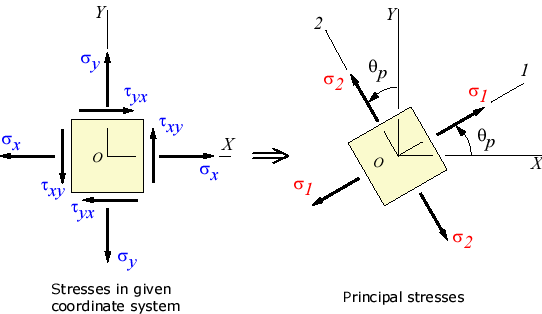
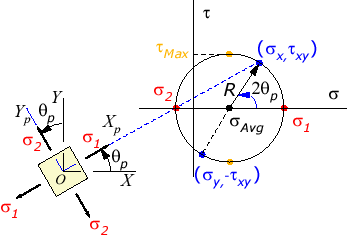
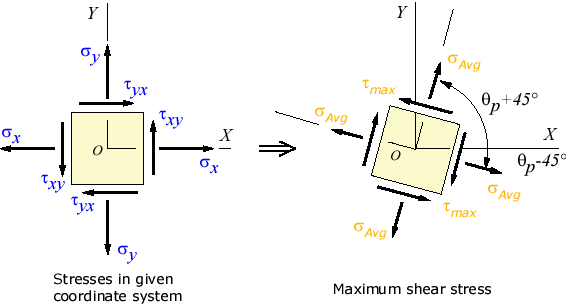
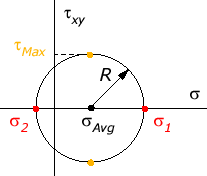
The Mohr's circle associated with the above stress state is similar to the following figure. However, the exact location of the center s_Avg, the radius of the Mohr's circle R, and the principal angle q_p may be different from what are shown in the figure.

Equations behind the Calculator

The formulas used in this calculator are,

Principal Stress
Need to find the principal stresses and their directions for a given input stress state? These calculators do the math for you for the case of Plane Stress and Plane Strain.

http://www.efunda.com/formulae/solid_mechanics/mat_mechanics/calc_principal_stress.cfm

Mohr's Circle

Introduced by Otto Mohr in 1882, Mohr's Circle illustrates principal stresses and stress transformations via a graphical format,

The two principal stresses are shown in red, and the maximum shear stress is shown in orange. Recall that the normal stesses equal the principal stresses when the stress element is aligned with the principal directions, and the shear stress equals the maximum shear stress when the stress element is rotated 45° away from the principal directions.

As the stress element is rotated away from the principal (or maximum shear) directions, the normal and shear stress components will always lie on Mohr's Circle.

Mohr's Circle was the leading tool used to visualize relationships between normal and shear stresses, and to estimate the maximum stresses, before hand-held calculators became popular. Even today, Mohr's Circle is still widely used by engineers all over the world.

The average stress, s_avg, and a "radius" R (which is just equal to the maximum shear stress),