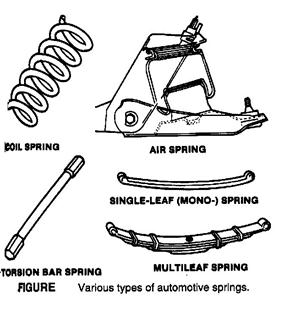
Springs

Springs are elastic members that exert forces, or torques, and absorb energy, which is usually stored and later released. The force produced by a spring can be compressive or tensile and linear or radial.

Springs are usually, but not necessarily, made of metal. Plastics can be used when loads are light. Modern structural composites are being introduced for some applications requiring minimum spring mass. Blocks of rubber often constitute springs, as in bumpers and in vibration isolation mountings of various machines such as electric motors and internal combustion engines. Pneumatic springs of various types take advantage of the elastic compressibility of gases, as compressed air in automotive "air shocks" and as hermetic ally sealed high-pressure nitrogen gas in the hydro-pneumatic suspensions of French Citroen automobiles. For applications requiring compact springs providing very large forces with small deflections, hydraulic springs have proved effective. These work on the basis of the slight compressibility of liquids, as indicated by their bulk modulus of elasticity. Product cost can sometimes be reduced by designing the required elasticity into other parts, rather than making those parts rigid and adding a separate spring.

Springs can be classified by the direction and nature of the force exerted when they are deflected. Several types of spring are listed in Table 1 according to the nature of force or torque exerted. The principal characteristics of various classes of springs are summarized in Table 2.

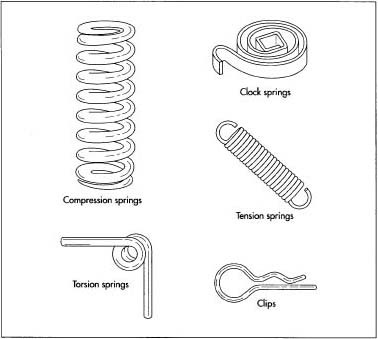
Table 1 Classification of springs according to the nature of force or torque exerted

Actuation	Type of spring
Compressive	Helical compression springs Belleville springs Flat springs, e.g. cantilever or leaf springs
Tensile	Helical extension springs Flat springs, e.g. cantilever of leaf springs Drawbar springs Constant force springs
Radial	Garter springs Elastomeric bands Spring clamps
Torque	Torsion springs Power springs

Table 2 Principle characteristics of a variety of types of spring

Type of spring	Principle characteristics
Helical compression springs	These are usually made from round wire wrapped into a straight cylindrical form with a constant pitch between adjacent coils
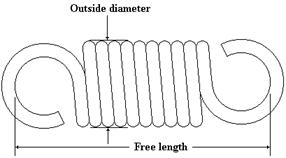
Helical extension springs	These are usually made from round wire wrapped into a straight cylindrical form but with the coils closely spaced in the no -load condition. As an axial load is applied the spring will extend but resisting the motion
Drawbar springs	A helical spring is incorporate into an assembly with two loops of wire. As a load is applied the spring is compressed in the assembly resisting the motion
Torsion springs	These exert a torque as the spring id deflected by rotation about their axis. A common example of the application of a torsion spring is the clothes peg
Leaf springs	Leaf springs are made from flat strips of material and loaded as cantilever beams. They can produce a tensile or compressive force depending on the mode of loading applied
Belleville springs	These comprise shallow conical discs with a central hole
Garter spring	These consist of coiled wire formed into a continuous ring so that they can exert radial inward force when stretched
Volute springs	These consist of a spiral wound strip, that functions in compression. They are subject to significant friction and hysteresis

Compression Spring:

Extension Spring

Torsion Spring

Spring design involves the relationship between force, torque, deflection, and stress. Springs have many uses in connection with machine design, such as to cushion impact and shock loading, to store energy, to maintain contact between machine members, for force measuring devices, to control vibration, and other related functions.

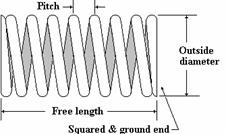
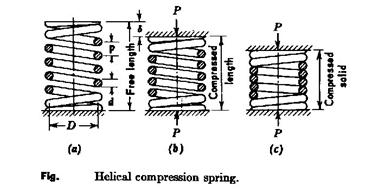
Helical springs

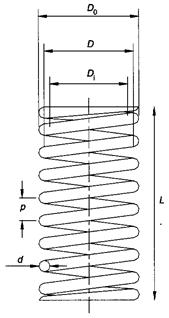
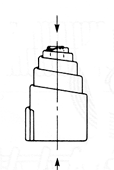
Figure 1(a) shows a helical coil spring with ends adapted to support a compressive load. At (b) the spring has been deflected by the axial load P, which may be assumed to compress the spring as between two parallel plates. The notation applies:

P       = axial load, N           D       = mean diameter of coil, mm                     = (Do + Di) / 2           d        = diameter of wire, mm                     = (Do – Di) / 2           p       = pitch of coils, mm           δ        = deflection of spring, mm           n        = number of active coils           C       = spring index = D/d = (Do-d)/d  = (4 : 12); less that 4 it is difficult to manufacture, more than 12 is likely to buckle.           G       = torsional modulus of                           elasticity, N/mm^2 τs = shearing stress, N/mm^2

  The number of active coils, n, represents the coils in the spring with the exception of those which lie flat against the compression plats. The inactive coils do not contribute to the deflection of the spring.

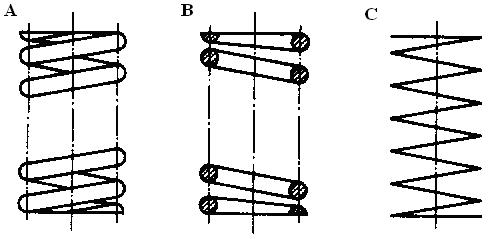
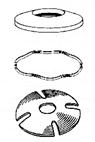
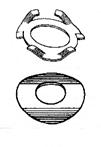
Springs (DIN ISO 2167)

Representation of a cylindrical helical compression spring made out of round wire.

A- in view

B- in section and

C- as name plate drawing

Stress in a helical spring made of round wire

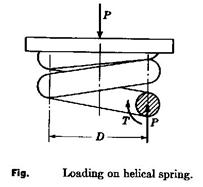
   Figure 2 shows a part of a compression spring that supports a compressive spring that supports a compressive load P and a section of the wire cut by axial plane. The part of spring shown in the figure is in equilibrium under the action of the two forces P and resisting torsional moment T. The torque equals

The shearing stress due to the torque T is

and the direct shearing stress is

where

and

for solid circle cross section

   The maximum shearing stress, which is located at the inner side of the curved wire, may determined by

where

is the direct shear factor

 It is evident form the above equation that for springs of small index C the effect of direct shear (1/2C) is appreciable.

   The effect of curvature of the wire as it forms the coil should be considered also.

   In order to include the effects of both direct shear and wire curvature, a stress factor had been determined by the use of approximate analytical methods developed by A. M. Wahl which may be used in the above equation to determine the maximum shearing stress in the wire as follows:

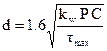
where

Deflection of helical spring

   An equation for the axial deflection of a helical spring in terms of the axial load, spring dimensions, and a materials constant may be conveniently determined by equating the work re3fquired to deflect the spring to the strain energy in the twisted wire. For close-coiled springs the bending of the wire is small and the strain energy of bending may be neglected.

   The axial load as shown in Fig. 2 increases linearly from zero to P, and hence the work required to compress the spring is the average force P/2 times the deflection, or Pδ/2.

   The strain energy in a bar twisted by a torsional moment T through a total angle θ is Tθ/2. The total angle of twist θ = TL/GJ, where L equals the length of the twisted wire and J equals the polar moment of inertia of the wire section. The active length of the wire in the helical spring equals (πDn/cos α), where α is the lead angle of the helix, which for close-coiled spring is of the order of 5^o; hence cos α is unity.

   For springs of indexes as used in machinery, namely, 2.5 or 3 and over, the strain energy in the curved wire forming the coils will be closed to the strain energy in a straight wire; hence from the above relations the following equation for δ may be obtain

where

          T = P D/2

          L = π D n

          J = π d⁴/32

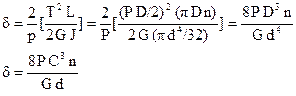
From the above equation

where (P/δ) is known as the spring rate. The spring rate represents the slope of the load-deflection line as shown in Fig. 3. Any difference between the ideal line and the actual curve is due principally to the change in number of active coils as the spring is deflected, to mechanical hysteresis of the material, and the friction between the end coils in contact with each other or with the loading plate.

   Compression springs in which the free length is more than four times the mean diameter of the coils may fail by sidewise buckling.   

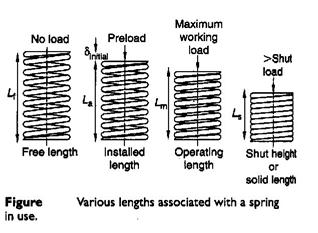
The spring rate for springs in parallel:

For springs having rates as shown in figure (a)

The spring rate for springs in series:

For springs having rates as shown in figure (b)

Nomogram for helical spring calculation:  (G = 81,400 MPa)

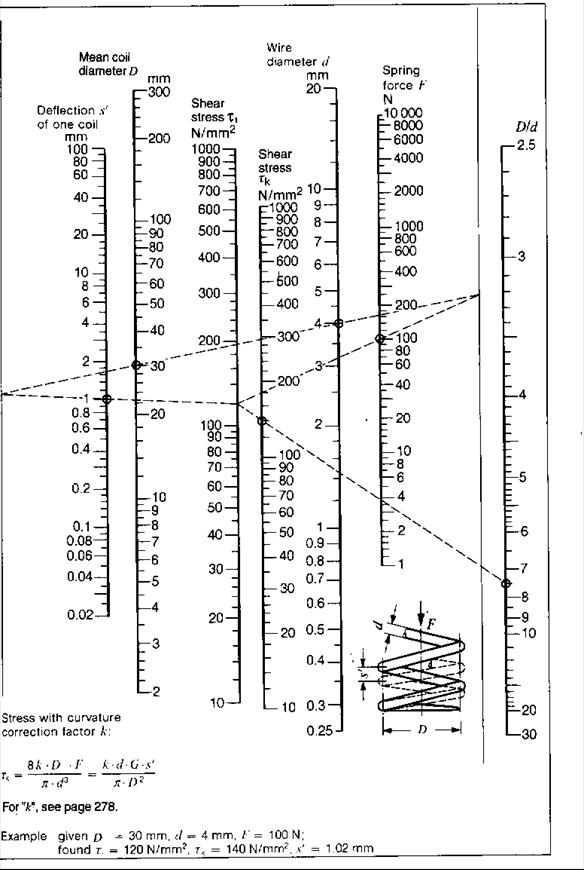
Explanation of the nomogram:

The Nomogram applies to cylindrical helical extension and compression springs made of round steel wire (shear modulus G=81,400 N/mm²). In the case of materials with a different shear modulus G^’ spring deflection must be multiplied by G/G^’.

The nomogram indicates the deflection s^’ of one coil. Total deflection s is obtained by multiplying (s^’) by the number of active coils n: s = n . s^’.

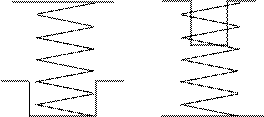
Spring ends:

   Helical spring ends may be either plain, plain ground, squared, or squared and ground as shown in Fig. 4 below. This results in a decrease of the number of active coils and affects the free length and solid length of the spring as shown below.

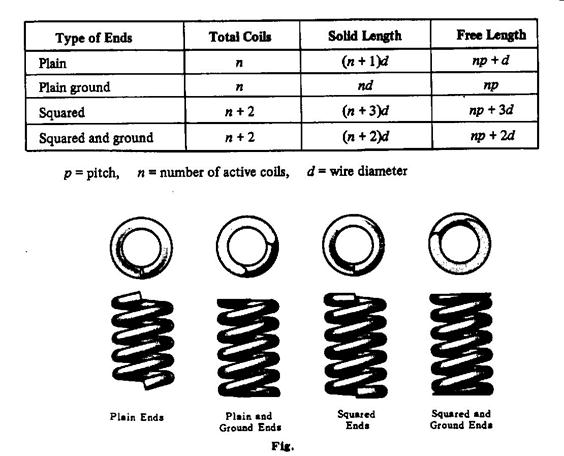
p=(D/3 : D/4), n= ( 3: 15)

Buckling:

Buckling may occur in compression springs if the free length is over 4 times the mean diameter unless the spring is properly guided. The critical axial load that will cause buckling may be approximated by

F_cr = k L_f K_L

where:

F_cr = axial load to produce buckling, N

          k = spring rate, N/m, of axial deflection

          L_f = free length of the spring, m

k_L = a factor depending on the ratio L_f/D (slenderness factor).

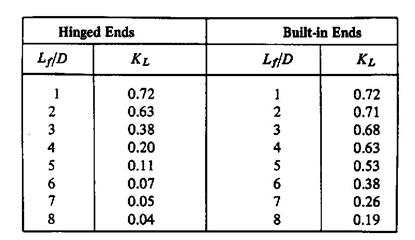
or L_f/D < 3 for no buckling

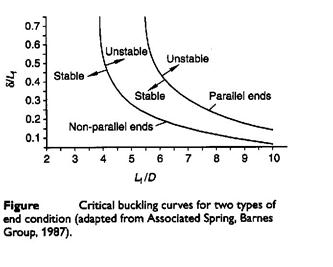Buckling depends on

L_f/D and δ/L_f

Buckling can be avoided by providing a spring guide

Allowable stresses:

For helical chrome-vanadium steel springs, oil-tempered, hot wound and heat-treated after forming, are tabulated below.

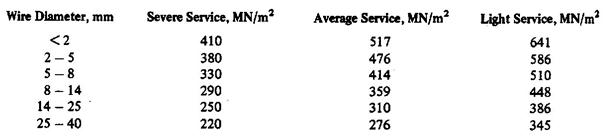
   Sever service includes rapid continuous loading where the ratio of minimum to maximum stress is one half or less. Average service is the same as severe except for intermittent operation. Light service includes springs subjected to static loads or to infrequently varied loads.

Spring design approach

· Specific material

· Guess a trail diameter (space available)

· Check spring rate and free length

- spring rate: k = (F_o-F_i) / (L_i-L_o)

- spring free length L_f = L_i + (F_i/k)

where:

F_o is the operating force, and L_o is the operating length

          F_i is the installed force, and L_i is the installed length 

Leaf Springs

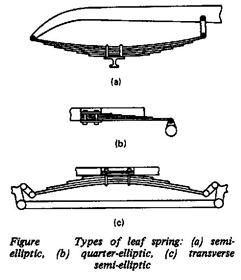Acts as:

- an elastic element

- guide

- damper

+ they are easy to manufacturer and convincement to repair

Disadvantage:

- large metal content (energy stored in unit volume in spring or torsion bar is 4 times more than a leaf spring; that lead to increase metal content).

- sufficient unsprung mass

- short service life.

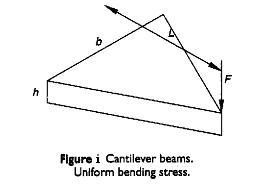
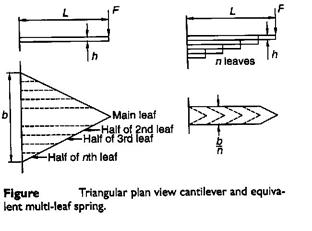
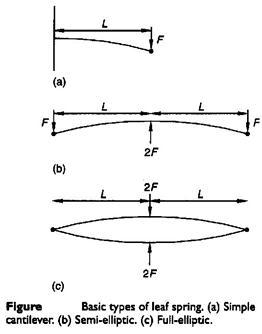
If it is desired to maintain uniform bending stresses over the length of the beam then the width of the cantilever needs to vary linearly with the location as illustrated in Figure i, (σ_b = M y/I = 12 F L y / b h³). The concept used in producing compact cantilever springs of uniform bending stress is to chop the triangular form illustrated in Figure i, into a number of strips and recombine them as illustrated in Figure ii. The multi-leaf spring shown and the single triangular section beam both have the same stress and deflection characteristics with the exceptions that the multi-leaf spring is subject to additional damping due to friction between the leaves and that the multi-leaf spring can carry a full load in only one direction due to the tendency for the leaves to separate. Leaf separation can be partially overcome by the provision of clips around the leaves.

The deflection of a triangular leaf spring is given by

where

          F is force (N)

          L is the length (m)

          E is the Young’s modulus (N/m²)

          I is the second moment of area (m⁴)

For a rectangular cross-section,

where b is width (m); and h is thickness (m).

The spring rate is given by

The corresponding bending stress (for cantilever, semi-elliptic and full-elliptic) is given by

For semi-elliptic beam the maximum deflection at the center is given by

For a full-elliptic beam the maximum deflection at the center is given by

* in the above equation the length b can be changed by nb^’ where n is the number of leafs and b^’ is the width of single leaf. The leaf width b^’ is chosen from the available range of rolled products. It is desired that the following condition should hold

          6 < b^’/h < 10

          6 <   n   < 14

The spring length can be determined using the equations for spring stiffness and stress to obtain

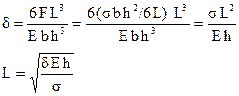
where

          δ = is the total deflection (δ_st + δ_d)

- Effect of adding an extra full length number of leaves (n_e) to the graduate length number of leaves (n_g):

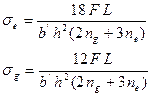
That means the extra leaves will have more stress than graduate ones.

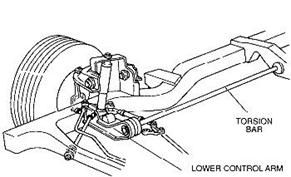
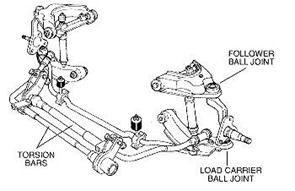
Torsion beam suspension (torsion bars)

Definition: A steel bar that is twisted to support the weight of the vehicle. Torsion bars are used in place of coil or leaf springs on some vehicles, and allow ride height to be adjusted to compensate for sage that occurs over time.

The bars are usually solid of circular cross section although hollow tubes and rectangular bars are used.

τ_all = 1000- 1050 MPa

The angle of twist and stiffness of a torsion bar are expressed as

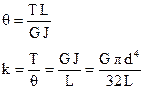
The torsion-bar working length L (without spline ends) is determined by the θ equation. It is recommended to choose the diameters and lengths of spline ends depending on the torsion-bar diameter

d_sp = (1.2 -1.3)d; and L_sp= (0.6-1.2)d

Suspension Formulae

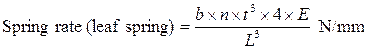
where b is the width of spring blade (m), L is the distance between the eyes of the spring when laden (m), t is the thickness of the blade (m), n is the number of blades, and E is the modulus of elasticity, which (modified to allow for internal friction) is 159 x 10⁶ kN/m².

    For a torsion bar, the spring rate is given as the twisting moment per angular deflection. When a lever is added, this can be converted into a rate for the vertical deflection of the end of the lever.

    Spring rate (torsion bar, for deflection at end of lever)

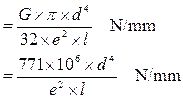
where G is the modulus of rigidity, which is 78.5 x 10⁶ kN/m² in this case, d is the diameter of the torsion bar (m), l is the effective length of the torsion bar (m), i.e. half the length of the bar for an anti-roll bar, and e is the length of the lever (m).

 Spring rate (coil spring)

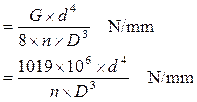
where G is the modulus of rigidity, which is 81.5 x 10⁶ kN/m² in this case, d is the wire diameter (m), n is the number of free coils, and D is the mean coil diameter (m). To find the number of free coils it is necessary to subtract the number of dead coils form the total number of coils. The dead coils are those that provide the abutment and so cannot be deflected, usually 1.5 to 2 coils.

Type

Configuration

Action

Helical Compression Round and Rectangular Wire		Push - wide load and deflection range - constant rate. Push - wide load and deflection range. Conical springs can be made with minimum solid height and with constant or increasing rate. Barrel, hourglass, and variable pitch springs used to minimize resonant surging and vibration.
Spring Washer Column 1: 1)Belleville 2)Wave 3)Slotted Column 2: 4)Finger 5)Curved		1) Push - high loads, low deflections - choice of rates (constant, increasing or decreasing) 2) Push - Light Loads, low deflection-uses limited radial space. 3) Push - Higher deflections than bellevilles. 4) Push - for axial loading of bearings. 5) Push - uesd to absorb axial end play.
Volute		Push - may have inherently high friction damping.
Beam 1) Cantilever, Retangular Section 2) Cantilever, Trapezoidal Section 3) Simple Beam	1 2 3	Push or pull - wide range of loads, low dflection range.
Helical Torsion Round or Rectangular Wire		Twist - constant rate.
Spiral 1) Hairspring 2) Brush	1 2	Twist Twist or Push
Constant Force Spring Motor Level Torque		Twist - exerts close-to-constant torque over many turns.
Helical Extension		Pull - wide load and deflection range - constant rate.
Drawbar		Pull - extension to a solid stop.
Constant Force		Pull - very long deflection at constant load or low rate.
Retaining Rings Round or Rectangular Wire		Pull or push - to resist axial loads.
Garter Springs 1) Extension 2) Compression	1 2	1) Pull with radial pressure. 2) Push with radial pressure.