Helical (Coil) Springs

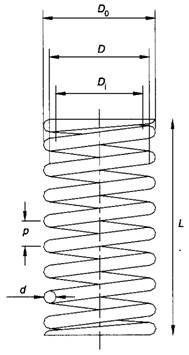
The figure shows a helical coil spring with ends adapted to support a compressive load. The notation applied are:

 

P       = axial load, N           D       = mean diameter of coil, mm                     = (Do + Di) / 2           d        = diameter of wire, mm                     = (Do – Di) / 2           p        = pitch of coils, mm           δ        = deflection of spring, mm           n        = number of active coils           C       = spring index = D/d = (Do-d)/d  = (4 : 12); less than 4; it is difficult to manufacture, more than 12; it is likely to buckle.           G       = torsional modulus of                          elasticity, N/mm2           τs            = shearing stress, N/mm2

 

Stresses on coil spring (t):

The coil spring wire is subjected to the following stresses:

a-     Torsional stress due to the load P

b-    Direct shear stress due to load P

c-     Torsional stress due to wire curvature

 

Torsional stress due to load P:

 

 

 

   In order to include the effects of both direct shear and wire curvature, a stress factor (K_w) had been determined by the use of approximate analytical methods developed by A. M. Wahl:

 

 

which may be used in the above equation to determine the maximum shearing stress in the wire as follows:

 

         

 

 

Various lengths associated with a spring:

 

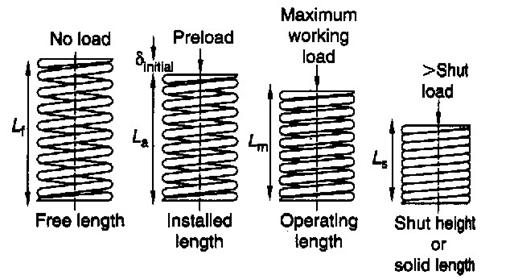
L_f = Free length

L_a = Installed length

L_m = Operating length

L_s = Shut height or Solid length

 

·        Compression springs in which the free length is more than four times the mean diameter of the coils may fail by sidewise buckling.  

 

Spring deflection (d):

 

         

Spring rate (stiffness) (k):

 

  

Spring ends conditions:

   Helical springs ends may be either plain, plain ground, squared, or squared and ground as shown in the figure below. This results in a decrease of the number of active coils and affects the free length and solid length of the spring as shown below.

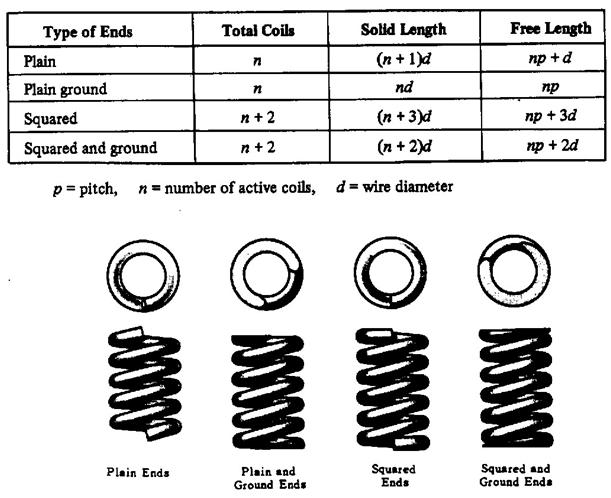
p=(D/3 : D/4), n= ( 3: 15)

 

 

Finding spring stress and deflection:

a-     Using the above equations of t_max , and d.

b-    Using the nomogram

c-     Using the Excel program given

 

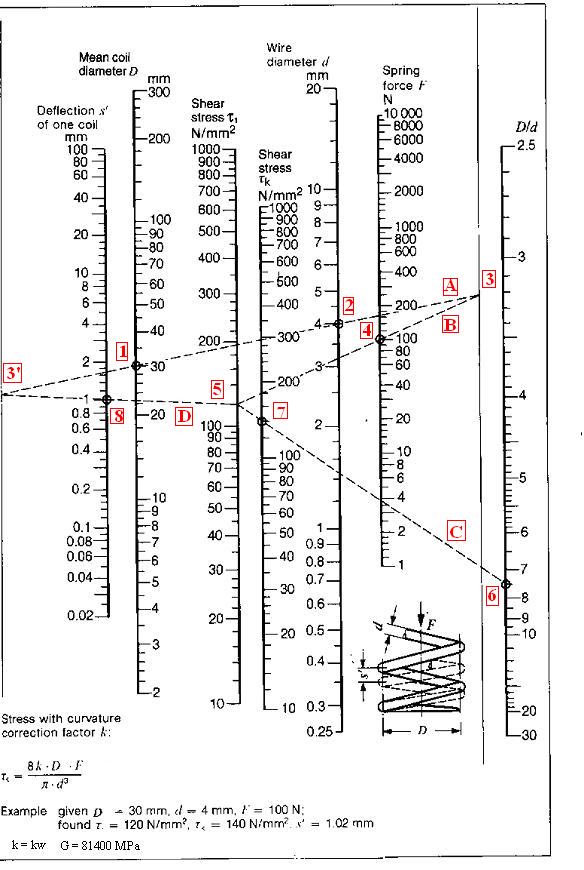
Explanation of the nomogram:

The nomogram applies to cylindrical helical extension and compression springs made of round steel wire (shear modulus G=81,400 N/mm²). In the case of materials with a different shear modulus G^’ spring deflection must be multiplied by G/G^’.

The nomogram indicates the deflection s^’ of one coil. Total deflection s (d) is obtained by multiplying (s^’) by the number of active coils n:

 

s (d) = n . s^’.

 

Example:

Find the stress and the deflection of a spring with the following dimensions:

D = 30 mm

d = 4 mm

F = P = 100 N

 

Solution steps:

1-   enter the value of D (point 1), and d (point 2) into the nomogram

2-   connect point 1, 2 with the line A and extend the line to points 3 and 3’ on either end.

3- enter the value of F (point 4) into the nomogram

4- connect point 3 to the value of the force F (point 4) with line B, extend the line B to point (5)

5- calculate the value of C and enter its value into the nomogram (point 6)

6- connect point 6 and 5 by line C to obtain point (7)

7- connect point 5 to point 3’ to obtain point (8)

 

Solution:

-         point 5 represents the value of t_t (MPa)

-         point 7 represents the value of t_max  (MPa)

-         point 8 represents the value of d’ = d/n (mm)

 

c- Excel Program:

 - enter the values of d, D, P, n, G.

The program will give you the values of C, K_w, t_t (Tau”) , t_max (Tau), d/n (Delta”), d (Delta), and K