Rod Deflection and Strain
Ex 1) A steel rod 1 m long and 20 mm x 20 mm in cross-sectional is subjected to a tensile force of 40 kN. Determine the elongation of the road, if modulus of elasticity for the rod material is 200 GPa.
|
Give: b = 20 mm h = 20 mm L = 1 m = 1 000 mm F = 40 kN = 40 000 N E = 200 GPa = 200 000 MPa
Req.: DL = ?
Solution: |
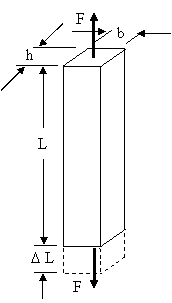 |
|
σ = F / A
A = b x h = 20 x 20 = 400 mm2
σ = F/A = 40 000/400 = 100 MPa
E = σ / e
e = DL / L
E = σ /(DL / L) = σ L / DL 200 000 = 100 x 1 000 / DL DL = 100 x 1 000 / 200 000 = 0.5 mm (Ans.) |
DL = 0.5 mm |
1) A load of 5 kN is to be raised with the help of a steel wire. Find the minimum diameter of the steel wire, if the stress is not to exceed 100 MPa. Also find the strain in the wire if its length is 2 m, if modulus of elasticity of the wire diameter is 220 GPa
2) In an experiment, a steel specimen of 13 mm diameter was found to elongate 0.2 mm in a 200 mm gauge length when it was subjected to a tensile force of 26.8 kN. If the specimen was tested within the elastic range, what is the value of Young’s modulus for the steel specimen?
3) A steel bar 2 m long and 150 mm2 in cross-section is subjected to an axial pull of 15kN. Find the elongation of the bar. Take E = 200 GPa.
4) A straight bar of 500 mm length has its cross-sectional area of 500 mm2. Find the magnitude of the compressive load under which it will decrease its length by 0.2 mm. Take E for the bar material as 200 GPa.
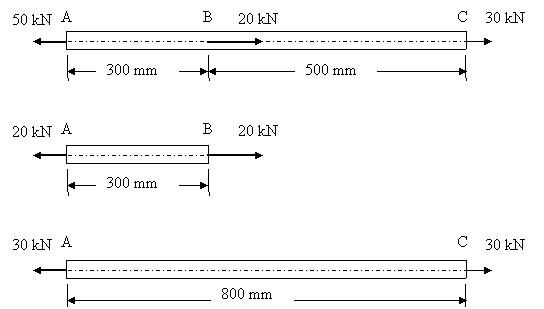
Ex 2) A steel bar of cress-sectional area of 200 mm2 is loaded as shown in the figure. Find the change in length of the bar. Take E as 200 GPa.
Given:
A= 200 mm2
E = 200 GPa = 200 000 MPa
Req.:
DL = ?
Solution
:
|
E = σ / e = (F/A) / (DL/L) = (F L) / (A DL)
DL1 = (F1 L1) / ( A E)
DL2 = (F2 L2) / ( A E)
DL = () / ( A E) + (F2 L2) / ( A E)
DL = 1 / (A E) (F1 L1 + F2 L2)
DL = [1/ (200 x 200 000)] (20 000 x 300 + 30 000 x 800)
DL = 0.75 mm (Ans.)
|
DL = 0.75 mm |
5) A brass bar, having cross-sectional area of 400 mm2 is subjected to axial forces as shown in the figure. Find the total elongation of the bar. Take E = 80 GPa.
