Definitions of Physical Quantities
A physical quantity is a physical property that can be quantified by measurement.
Classification of physical quantities:
Scalars and vector quantities:
Scalars are quantities that have
magnitude only; they are independent of direction.
Vectors
have both magnitude and direction. The length of a vector represents
magnitude. The arrow shows direction.
Typical examples of scalar quantities are time, speed, temperature, and volume. A scalar quantity or parameter has no directional component, only magnitude. For example, the units for time (minutes, days, hours, etc.) represent an amount of time only and tell nothing of direction. Additional examples of scalar quantities are density, mass, and energy, work, pressure..
Normal mathematical operation can be applied on scalar quantity.
Typical examples of vector quantities are displacement, velocity, force, momentum, acceleration.
When doing any mathematical operation on a vector quantity (like adding, subtracting, multiplying ..) you have to consider both the magnitude and the direction.
Symbols for physical quantities:
Usually, the symbols for physical quantities are chosen to be a single
letter of the Latin or Greek alphabet, and are often printed in italic type.
Often, the symbols are modified by subscripts and superscripts, to specify what
they refer to - for instance Ek is usually used to denote
kinetic energy and cp heat capacity at constant pressure.
Units of physical quantities:
Most physical quantities Q include a unit. Neither the name of a physical quantity, nor the symbol used to denote it, implies a particular choice of unit.
Dimensional analysis:
Technique used in the physical sciences and engineering to reduce physical properties such as acceleration, viscosity, energy, and others to their fundamental dimensions of length (L), mass (M), and time (T). This technique facilitates the study of interrelationships of systems (or models of systems) and their properties. Acceleration, for example, is expressed as length per unit of time squared (LT-2); whether the units of length are in the English or metric system is immaterial. Dimensional analysis is often the basis of mathematical models of real situations.
Time (t)
The fundamental unit of time suggested by the International System of Units
is the second, since 1967 defined as the second of International Atomic Time,
based on the radiation emitted by a Caesium-133 atom in the ground state.
Based on the second as the base unit, the following time units are in use:
* minute (1 min) = 60 s
* hour (1 h) = 60 min = 3.6 ks
* Julian day (1 day) = 24 h = 86.4 ks
Displacement and Distance (L)
Displacement is measured in meters (m), or sometimes more conveniently in kilometers, millimeters or centimeters. Distance (scalar) is the magnitude of the displacement (vector).
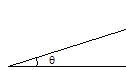
Angle (θ)
|
Angle is the figure formed by two rays sharing a common endpoint, called the vertex of the angle. The magnitude of the angle is the "amount of rotation" that separates the two rays, and can be measured by considering the length of circular arc swept out when one ray is rotated about the vertex to coincide with the other. The degree and the radian are by far the most common. The turn (or full circle, revolution, rotation, or cycle) is one full circle. 1 turn = 360° = 2π (rad) |
|
Area (A)
Any flat, curved, or irregular expanse of a surface. It is measured in meter square (m2).
Volume (V)
The volume of any solid, liquid, gas, plasma, or vacuum is how much three-dimensional space it occupies, often quantified numerically. It is measured in cubic meter (m3) or liter (l).
1 l = 1000 cm3 = 0.001 m3
Velocity (v) and Speed
Velocity is measured as meters per second (m/s), or sometimes more conveniently as kilometers per hour (km/h). Useful conversions are 1 m/s = 3.6 km/h and 0.278 m/s = 1 km/h). The speed is the magnitude of the velocity vector.
v = dL/dt [m/s]
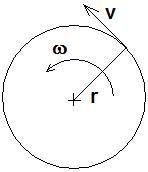
Angular velocity (ω)
Angular velocity is a measure of the angular displacement per unit time.
ω = dθ/dt [rad/s] (1/s)
The angular velocity can be measured in revolution per minute (rpm).
ω = 2 π N/60
Where:
N = revolution per minute (rpm)
|
Angular and linear velocity The linear velocity of a particle is related to angular velocity by : v = ω r
v = (2 π N/60) r
|
|
Acceleration (a)
Acceleration or deceleration is the rate of change of speed. It is measured as meters per second per second or m/s2.
a = dv/dt [m/s2]
An increase in velocity from 36 km/h to 72 km/h during 4 s (that is from 10 m/s to 20 m/s) is an average acceleration of 2.5 m/s every second or 2.5 m/s2
If the speed increases from u m/s (initial velocity) to v m/s (final velocity) during t seconds (time), then the average acceleration a m/s2 is given by
a = (v-u)/t m/s2
Acceleration due to gravity (g)
In a vacuum all freely falling bodies, whatever their size, shape or mass, have the same acceleration at a given place. This acceleration, given the symbol g since it is due to the force of gravity, has the value of about 9.81 m/s2 at sea level near London, 9.78 m/s2 at the equator, and 9.83 m/s2 at the poles. In physics, gravitational acceleration is the acceleration on an object caused by gravity, a conventional standard value of exactly 9.80665 m/s2 (g = 9.81 m/s2)
The acceleration of objects falling in the atmosphere depends on their wind resistance. For example, depending on the conditions, the human body reaches a terminal velocity of some 200 km/h, when the wind resistance equals the force of gravity and no further acceleration can occur. A motor vehicle is also subject to wind resistance.
*
Car acceleration and deceleration indication
Another way to indicate the car acceleration is the time taken by the
car form 0 velocity to reach 100 km/h, or (0- 60 mph). Example: 0- 100 km/h in
4 s. For comparison, an object in free fall (without any
air resistance) has an acceleration time from 0–100 km/h of 2.83 seconds.
A convenient way to measure braking action is to equate (compare) vehicle deceleration to the gravity acceleration constant [g]. Example: declaration = 0.3 g.
Angular acceleration (α)
Angular acceleration is the rate of change of angular velocity over time. In SI units, it is measured in radians per second squared (rad/s2).
α = dω/ dt = d2θ/ dt2
Mass (m) and weight (w)
A 'body' contains a certain amount of stuff or matter called mass. The unit of mass is the kilogram (kg).The pull of earth -the force of gravity- acting on this mass is the weight of the body. Owing to its mass a body has inertia, that is, it resists being accelerated or decelerated and will remain at rest or continue moving at a uniform speed in a straight line unless acted upon by an external force.
w = mg
where
w = the weight in newtons (N),
m = the mass in kilograms (kg),
g = the acceleration of falling body due gravity in meter per second square (m/s2)
Mass
moment of inertia (I)
In classical
mechanics, moment of inertia, also called mass moment of
inertia, rotational inertia, or the angular mass, (SI units kg·m2) is a measure of an
object's resistance to changes to its rotation. It is the inertia of a rotating
body with respect to its rotation. The moment of inertia plays much the same
role in rotational dynamics as mass does in linear dynamics,
describing the relationship between angular momentum and angular velocity, torque and angular acceleration, and several other quantities.
A simple definition of the moment of inertia (with respect to a given
axis of rotation) of any object, be it a point mass or a 3D-structure, is given
by:
![]()
where m is mass and r is the perpendicular distance to the axis of rotation.
Force (F)
The force is a measurable influence tending to cause movement of a body (its intensity). The unit of force is newton, 1 newton is the value of a force which if exerted upon one kilogram gives it an acceleration of 1 m/s2.
F = m a,
1 N = (1 kg) (1 m/s2) = 1 kg m/s2
where
F = force (newton)
m = mass (kg)
a = acceleration (m/s2)
There are different types of forces; external force, internal force, friction force, and reaction force.
Inertia force (Fi)
All bodies have inertia -the tendency to remain at rest or in uniform motion. For example, when a piston is decelerated from maximum speed to a dead centre position and accelerated in the opposite direction, it exerts an inertia force on the connecting rod.
The value of the inertia force depends upon the mass of the body and
the acceleration or deceleration:
F = ma
where F= force in newtons (N), m = mass in kilograms (kg), and a = acceleration or
deceleration in (meters/second)/second (m/s2).
Thus to reduce the inertia forces produced by the reciprocating parts, their mass must be kept as small as possible.
* The equivalent Newton's second law for rotation is, thus :
T = I α
where
T = torque (N m)
I = mass moment of inertia (kg m2)
α = angular acceleration
[rad/s2] (1/s2)
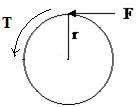
Centrifugal force
A moving body travels in a straight line at uniform speed unless acted upon by an external force. If made to travel in a circle, the body exerts centrifugal force acting outwards from the centre upon the constraining member. The equal and opposite constraining force is termed centripetal.
CF = m v2/r
= m ω2 r
where
CF = centrifugal force in newtons (N),
m = mass in kilograms (kg),
v = ω r
v = linear velocity in meters/second (m/s),
r = radius of curvature in meters (m) and
ω = angular velocity in radians/second [rad/s] (1/s), where 1 revolution = 2π (radian).
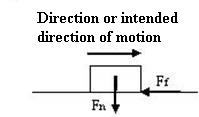
Friction force (Ff)
It is found that the horizontal force required to drag a body
over a smooth, level, dry surface is approximately a constant fraction of the
perpendicular force between the surfaces. In the figure, w is the load or
the
normal force Fn between the surfaces, and Ff is the force
parallel to the contact surfaces and is called the friction force.
The ratio Ff / Fn , fairly constant for any given combination of two materials, is termed the coefficient of friction µ. The value of µ depends upon the materials and the condition of the surfaces and not greatly upon the speed or area of contact.
|
|
Ff = μ Fn
where
Ff = friction force (N)
Fn= normal force (N)
μ = coefficient of friction = Ff /Fn
In some cases - brakes, drive belts, clutch, tires - a high coefficient of friction is required, whilst in others, such as bearings, a low coefficient is necessary.
The friction force reaches a maximum value just before sliding occurs; this is static friction or stiction. It then reduces to a lower dynamic or kinetic value during sliding. The difference between these two values can have important results, e.g. during a cornering 'breakaway' when the centrifugal force exceeds the limit of the static friction force.
The coefficient of friction between the tires and the road may be almost zero under icy conditions. Alternatively, some braking distances indicate a coefficient exceeding 1.0, i.e. the frictional force is greater than the weight of the vehicle. Some interlocking between the tires and the road takes place where tread rubber is torn away.
When surfaces are separated by a film of lubricant, fluid friction rather than dry friction is involved. This viscous friction is related to the area of contact, the speed and the viscosity of the lubricant.
Table 1: Materials coefficients of static friction
|
Materials |
Coefficient of static friction |
|
Leather on cast iron |
0.4- 0.6 |
|
Friction material on cast iron |
0.35- 0.45 |
|
Cast iron on cast iron |
0.2- 0.3 |
|
Smooth greased wooden 'skids' |
0.05- 0.08 |
|
Plain bearing fluid friction |
0.02- 0.04 |
|
Ball bearing |
0.00- 0.004 |
Principle of moments
When a body is at rest or in equilibrium (a state of balance), the sum of the clockwise turning moments about any axis, real or imaginary, is equal to the sum of the anticlockwise moments about the same axis.
Were this not the case, the unbalanced moment would cause the body to rotate about the chosen axis.
Centre of gravity (CG)
The centre of gravity (CG) of a body can be regarded as the point where, if the whole weight of the body were concentrated, it would produce a moment of force about any axis equal to the sum of the moments of force of each part of the body about the same axis. When inertia force is involved the centre of gravity becomes the centre of mass.
Couple (M)
When two equal forces act on a body so that their lines of action are parallel but opposite in direction, they form a couple tending to rotate the body.
The torque produced by a force acting on a pivoted body can be regarded as the result of a couple formed by the original force and an equal and opposite reaction at the pivot (see the Figure).
|
A couple can only be balanced by another couple of equal value acting in the opposite direction of rotation and not by a single force.
|
|
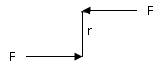
Torque (T)
When a force acts on a body pivoted on a fixed axis, the
product of the force perpendicular to the radius, and the radius at which it
acts, is termed the turning moment of the force or torque. Torque is measured
in newton meters (N m) (to distinguish it from work).
T = F r
|
where |
|
Work (W)
Work is done when a force overcomes resistance and causes
movement. Work is measured by the product of the force and the distance moved
in the direction of the force, the unit being the joule (J):
W = F s
Where:
W = work done in joules (J),
F = force in newton (N), and
s = distance in meters (m) moved in the direction of
the force.
If the force causes no movement, then no work is done, or if the force in the apposite direction of the movement, then the work is negative.
Power (P)
Power is the rate of doing work. The unit, the watt, is a rate
of working of 1 joule per second (1 J/s)
power = work done per second = [W / t] {N m /s}, {J/s}, (W)
The relation between power and torque
If a tangential force is applied to a shaft, then the work done per one revolution is:
W = F s = F (2 π r) = (2 π) T
Since the power is
P = W/t = (2 π / t) T
P = ωT
P = (2 π N/60) T
Where:
P = power (W)
W = work (J)
t = time (s)
F = force (N)
s = displacement
(m)
T = torque (N m)
ω = angular
velocity [rad/s] (1/s)
N = rev per min (rpm)
Using these formulae, the power can be calculated from the torque and speed of a shaft.
Temperature (t)
Temperature is a physical property of matter that quantitatively expresses the
common notions of hot and cold. Objects of low temperature are cold, while
various degrees of higher temperatures are referred to as warm or hot.
Quantitatively, temperature is measured with thermometers, which may be
calibrated to a variety of temperature scales.
The International System of Units (SI) defines a scale and unit for the
thermodynamic temperature by using the kelvin temperature. The unit symbol of
the kelvin is K. While the Kelvin scale is the principal temperature scale for
use in science and engineering, much of the world uses the Celsius scale (°C)
for most temperature measurements. It has the same incremental scaling as the
Kelvin scale, but fixes its null point, at 0°C
= 273.15K,
the freezing point of water, while water boils at 100 °C = 373.15 K. Few
countries, most notably the United States, use the Fahrenheit scale for common
purposes, a historical scale on which water freezes at 32 °F and boils at 212
°F.
Fahrenheit = Celsius * 9 / 5 + 32
Celsius = (Fahrenheit - 32) * 5 / 9
1 K = 1°C = 1.8 °F = 1.8 °R
Density (ρ)
Density is the mass of a substance per unit volume (kg/m3). The
density of water is, for practical purposes, 1000 kg/m3 or 1 kg/l.
(The litre (l) is 10-3 m3.)
The density of solids and liquids are usually stated in g/cm3, while gases are usually in kg/m3.
|
State |
Material |
Density |
|
Liquids |
|
|
|
|
Mercury |
13.6 |
|
|
Seawater |
1.03 |
|
|
Water |
1.00 |
|
|
Ethyl alcohol |
0.81 |
|
Solids |
|
|
|
|
Gold |
19.3 |
|
|
Iron |
7.8 |
|
|
Aluminum |
2.7 |
|
|
Ice (0 °C) |
0.92 |
|
Gases |
(at normal pressure and |
Density |
|
|
Air (0 °C) |
1.29 |
|
|
Air (10 °C) |
1.25 |
|
|
Hydrogen (0 °C) |
0.090 |
|
|
Helium (0 °C) |
0.178 |
Relative density or specific gravity
relative density of the substance = (mass of a substance / mass of an equal volume of water)
This ratio is called the relative density of the substance, and represents how many times it is heavier or lighter than the same volume of water. Note that relative density has no units. Example of substances relative densities (oxygen = 0.0014, steel=8.0, lead =11.4, mercury = 13.6).
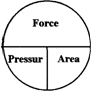
Pressure (p)
Pressure is the force per unit area; the unit is N/m2
or the Pascal (Pa). Larger practical units are kN/m2 (kPa) and MN/m2
(MPa). Note that
1 MN/m2 (MPa) = 1N/mm2
A pressure of 7 MPa means that each mm2 subject to the pressure has a force of 7 N acting on it, and the total force on the surface will be the product of the pressure and the area:
|
pressure = force/ area
force = pressure x area |
|
Atmospheric pressure
Air has weight. The atmosphere above the earth produces a
pressure at sea level of approximately 1 bar, where 1 bar = 105 N/m2
or 105 Pa. Standard atmospheric pressure (atm)
is 1.01325 bar, 1013.25 millibar or
101.325 kPa. Also:
1 atm = 760 mm Hg (Torr) (mercury column) = 10333 mm H2O (water column)
Above sea level the atmospheric pressure will be less than 1 bar.
Gauge and absolute pressure
The ordinary pressure gauge gives readings measured above
atmospheric pressure. To obtain the absolute pressure, that is the pressure
measured above a perfect vacuum, atmospheric pressure must be added to the
gauge reading:
absolute pressure = gauge pressure + atmospheric pressure
Stress (σ,
τ)
Components may be subject to a tensile load, as in a
brake cable; a compressive load, as in a push rod; or a shear load,
as in a shackle pin. In each case the value of the stress produced is found by
dividing the load by the cross-sectional area on which it acts. Typical units
of stress are N/m2 (Pa), kN/m2 (kPa) and MN/m2
= N/mm2 (MPa) .
For tensile and compressive stress the cross-sectional area is measured at right angles to the direction of the force, while for shear stress the area is measured parallel to the direction of the force.
Energy (E)
In all such energy transformation processes, the total energy remains the same.
Energy may not be created nor destroyed.
Any form of energy can be transformed into another form. When energy is in a form other than heat, it may be transformed with good or even perfect efficiency, to any other type of energy. With thermal energy, however, there are often limits to the efficiency of the conversion to other forms of energy, due to the second law of thermodynamics.
Throughout the history of science, energy has been expressed in several different units such as ergs and calories. At present, the accepted unit of measurement for energy is the SI unit of energy, the joule. In addition to the joule, other units of energy include the kilowatt hour (kW h) and the British thermal unit (Btu). These are both larger units of energy. One kW h is equivalent to exactly 3.6 million joules, and one Btu is equivalent to about 1055 joules.
There are different types of energies; kinetic, potential, mechanical, thermal, chemical, electric, and nuclear energy.
Free body diagram
1- Identify the object of interest.
2- Isolate the object of interest.
3- Draw the weight of the object as downward vertical force vector.
4- Identify all the individual interaction forces acting on the object, and draw them as force vectors on a free-body diagram.
5- Choose a convenient coordinate system, and draw the coordinate axles on the free body diagram.
6- Write the components of the vector equation in the chosen coordinate system (using the free body diagram).
7- Write the dimensions of the body
8- Solve the equations for whatever quantities the problem asks for.
Equilibrium Equations
The body is considered in equilibrium state if the following equations are satisfied.
Σ Fx = 0
Σ Fy = 0
Σ Fz = 0
Σ M @ any point = 0
where F = force, M= moment, and x, y, z are three arbitrary perpendicular axis.
Center of Gravity CG (Center of Mass CM)
Center of Gravity, is the point at which all of the weight of an object appears to be concentrated. If an object rotates when thrown, the center of gravity is also the center of rotation. When an object is suspended so that it can move freely, its center of gravity is always directly below the point of suspension. An object can be balanced on a sharp point placed directly beneath its center of gravity. It is important for automobiles and trucks to have their centers of gravity located close to the road, because a low center of gravity gives them stability
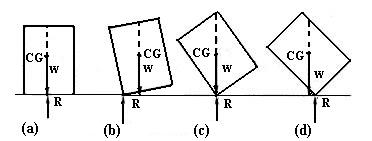
Types of equilibrium
Consider a block of steel (as shown in the figure) on a bench. In position (a) the block is in equilibrium and is considered to be in a stable condition. Its weight acting downwards is supported by the reaction of the bench. If the block is tilted as in (b) the block is acted upon by two forces, the reaction at the point of contact x and the weight W acting through the centre of gravity CG which will return the block to its stable position. If the block was tilted to a position (c) where W and the reaction R are equal and opposite, this would be considered as unstable equilibrium, and any further tilt would result in the force W acting to the left of the pivot point x (in the figure (d)). The block would then topple over. It may be noted that as the block is tilted from position (a) to position (c) the point of CG is rising and stable conditions exist, but beyond position (c) the CG begins to lower and unstable conditions exist.