Mechanics 1
Mechanics can be defined as that branch of the physical sciences concerned with the state of rest or motion of bodies that are subjected to the action of forces. A thorough understanding of this subject is required for the study of structural engineering, machine design, fluid flow, electrical instrumentation, and even the molecular and atomic behavior of elements.
In general, mechanics is subdivided into three branches: rigid-body mechanics, deformable-body mechanics, and fluid mechanics. In this course only rigid-body mechanics will be studied.
Rigid-body mechanics is divided into two areas: statics and dynamics. Statics deals with the equilibrium of bodies, that is, those which are either at rest or moving with a constant velocity; whereas dynamics is concerned with the accelerated motion of bodies. Statics can be considered as a special case of dynamics, in which the acceleration is zero.
Historical Development
The subject of statics developed very early in history, the writings of Archimedes (287-212 B.C.) provide an explanation of the equilibrium of lever.
Since the principles of dynamics depend upon an accurate measurement of time, this subject developed much later. Galileo Galilei (1564-1642) was one of the major contributors in this field. His work consisted of experiments using pendulums and falling bodies. The most significant contributions in dynamics, however, were made by Isaac Newton (1642-1727), who is noted for his formulation of the three fundamental laws of motion and the law of universal gravitational attraction. Shortly after these laws were postulated, important techniques for their application were developed by Euler, D’Alembert, Lagrange, and others.
Newton’s Three Laws of Motion.
First Law: A particle originally at rest, or moving in a straight line with constant velocity, will remain in this state provided the particle is not subjected to an unbalanced force.
Second Law: A particle acted upon by an unbalanced force F experiences an acceleration a that has the same direction as the force and a magnitude that directly proportional to the force. If F is applied to a particle of mass m, this law may be expressed mathematically as:
F = ma
Third Law: For every force acting on a particle, the particle exerts an equal, opposite, and collinear reactive force.
Particle. A particle has a mass but essentially has no size or shape,
Rigid body. A rigid body can be considered as a combination of a large number of particles in which all the particles remain at a fixed distance from one another both before and after a load is applied.
Concentrated Force. A concentrated force represents the effect of a loading which is assumed to act at a point on a body.
Physical
quantity
Most physical quantities can be expressed mathematically by means of
scalars and vectors.
Scalar. A quantity possessing only a magnitude is called scalar.
Vector. A vector is a quantity that has both a magnitude and directions. A vector is represented graphically by an arrow, which is used to define its magnitude, line of action, and direction.
Types of vectors:
| a | A fixed vector |
|
| b | Sliding vector |
|
| c | Free vector | |
| d | Equal vectors |
|
| e | Negative vector |
|
| f | Coplanar vectors |
|
| G | Concurrent vectors |
|
| h | Collinear vectors |
|
Vector Addition
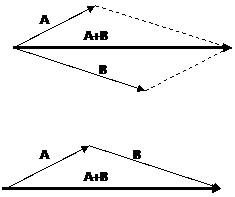 |
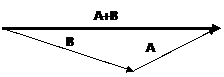 |
Multiplication and Division of a Vector by a Scalar
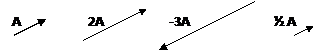 |
Vector Addition of Forces Using the Parallelogram law
Two common problems in statics involve either the determination on the magnitude and direction of the resultant force FR, given the components forces F1 and F2 acting at point O, or the determination of the magnitude and/or directions of the components F1 and F2, given the resultant force Fr. Both of these problems require application of the parallelogram law.
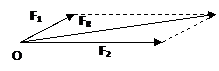 |
If more than two forces act at point O, successive applications of the parallelogram can be carried out in order to obtain the resultant force.
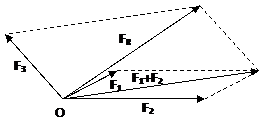 |
Procedure
for analysis
Problems that involve the addition of two forces and contain at most
two unknown can be solved using the following procedure:
|
Sine law: |
|
|
|
Cosine law:
|
|
Addition of Rectangular Force Components
If a force F lies in the x-y plane, its projection of the force along the x and y axes yields its two components Fx and Fy. By the parallelogram law,
F = Fx + Fy
In order to simplify the operations of vector algebra, we will represent F in Cartesian vector form. To do this the rectangular component will be designated as Fx and Fy, which is always positive. Their directions will be specified using Cartesian unit vectors i, j, which are directed along the x and y axes, respectively. The unit vector have a magnitude of one (dimensionless) unit and are positive or negative depending upon whether they are pointing along the positive or negative x or y axis. Multiplying i, j by the scalars Fx, Fy and adding the results yields F expressed as a Cartesian vector, namely,
F = Fx i + Fy j
 |
 |
Resultant of several coplanar forces
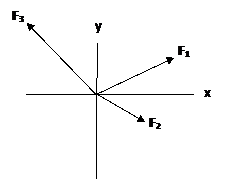 |
 |
FR = F1 + F2 + F3
= [F1x i + F1y j] + [F2x i – F2y j] + [-F3x i +F3y j]
= [F1x + F2x – F3x] i + [F1y – F2y + F3y] j
In the general case, the resultant of any number of forces can be represented symbolically as
FR = S F = FRx i + FRy j
Where the components have magnitudes of
FRx = S Fx, FRy = S Fy
Once the x and y component of FR have been determined, the magnitude of FR can be calculated from the Pythagorean theorem , that is
![]()
If the angle q is used to specify the direction of FR, then by trigonometry,
![]()
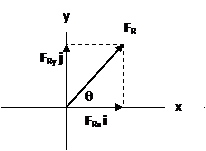 |
