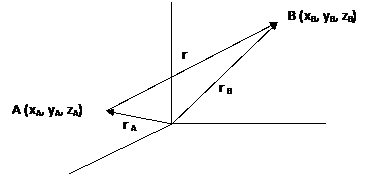Mechanics 2

Force Resultants in Three Dimensions

Force Expressed as a Cartesian Vector

If a force lies in an octant of an x, y, z frame, it may be resolved into three rectangular components. By successive application of the parallelogram law yield F = F ^’ + F_z, and F ^‘ = F_x + F_y. Combining these two equations, we have

F = F_x + F_y + F_z

If a set of i, j, k, unit vector is used to define the positive direction of the x, y, z axes. F can be expressed in Cartesian vector form as

F = F_x i + F_y j +F_z k

Here, F_x , F_y , F_z represent the magnitude of each force component and i, j, k specify the components’ direction.

Magnitude of Force

Direction of Force

These numbers are known as the direction cosines of F. Once they have been obtained, the direction angles  α, β, γ can then be obtained from the inverse cosines.

Where             cos² α + cos² β + cos² γ = 1

Unit vector (u)

The unit vector is dimensionless,

F = F u    and

k

And

Position Vectors

This vector is of importance in formulating a Cartesian force vector directed between any two points in space, and it will be used in finding the moment of a force. The position vector r is defined as a fixed vector which locates a point in space to another point, 

                                    r_A + r = r_B

                                    r = r_B - r_A

                                    r = (x_B i + y_B j + z_B k)- (x_A i + y_A j + z_A k)

r = (x_B - x_A)i + (y_B - y_A)j + (z_B - z_A)k

Force vector directed along a line

We can formulate F as a Cartesian vector by realizing that it acts in the same direction as the position vector r directed from point A to point B on the cord.

Thus common direction is specified by the unit vector

u  = r /r

F = F u = F (r/r)

Procedure for analysis

When F is directed along a line which extends from point A to point B, then F can be expressed in Cartesian vector form as follows:

Position vector
 Determine the position vector r directed from A to B, and compute its magnitude r.

Unit vector
Determine the unite vector u = r/r which defines the direction of both r and F.

Force vector
Determine F by combining its magnitude F and direction u, i.e., F = F u.

* Example:

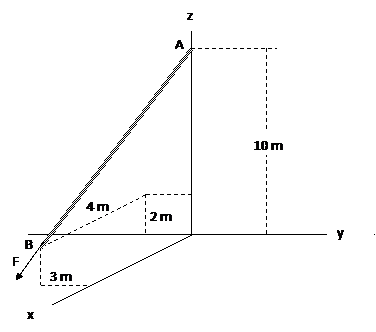
A man pulls on the cord shown in the figure with a force of 300 N.  Represent this force, acting on the support A, as a Cartesian vector and determine its direction. 

Position vector
The coordinates of the end points of the cord are A(0, 0, 10), B(4, -3, 2). The position vector from A to B is:

r = (4 – 0)i + (-3 – 0)j + (2 – 10)k

                                      = {4i - 3 j - 8 k} m

The magnitude of r, which represents the length of cord AB, is

Unit vector

Force vector

Ans.

The coordinate direction angles are measured between r (or F) and the positive axes of localized coordinate system with origin placed at A. From the components of the unite vector.

                            Ans.

                          Ans.

                          Ans.