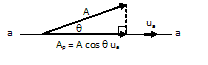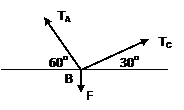Mechanics 3
Dot Product
Occasionally in statics there is a need to be able to project a force along given axis or to find the angle between two lines. The dot product defines a particular method for “multiplying” two vectors and is used to solve the above-mentioned problems, especially in three dimensions.
The dot product of two vectors A and B, written A . B, read “A dot B,” is defined as the product of the magnitudes of A and B and the cosine of the angle q between their tails.
|
|
Expressed in equation form,
A . B = AB cos q (1)
where 0o £ q £ 180o. The dot product is often referred to as the scalar product of vectors, since the result is a scalar and not a vector.
Laws of Operation
1- Commutative law: A . B = B . A
2- Multiplication by a scalar:
m (A . B) = (mA) . B = A . (mB) = (A . B) m
3- Distributive law:
A . (B +D) = (A . B) + (A . D)
Cartesian Unit Vector Formulation
Equation (1) may be used to find the dot product of each of the Cartesian vectors. For example,
i . i = (1) (1) cos 0o = 1. In a similar manner,
i . i = 1 k . k = 1 j . k = 0 i . k = 0 j . k = 0
j . j = 1 i . j = 0 k . i = 0 j . i = 0
Cartesian Vector Formulation
A . B = (Axi + Ayj + Azk) . (Bxi + Byj + Bzk)
A . B = Ax Bx + Ay By + Az Bz (2)
Applications
The dot product has two important applications in mechanics.
1. The angle formed between two vectors or intersecting lines. The angle q between vectors A and B is determined from equation (1) and written as
![]() 0 £ q £ p
0 £ q £ p
Here A . B is computed from equation (2).
2. The projection of a vector along an axis. The projection of a vector A along the aa axis is defined by Ap, where the magnitude is Ap = A cos q. If the aa axis is specified by the unit vector ua , then, since ua = 1, we can determine Ap directly from the dot product equation (1), i.e.,
|
|
Ap = A cos = A . ua
The projected vector Ap is therefore represented as
Ap = A cos q ua = (A . ua) ua
Equilibrium of a particle
Here the methods of resolving a force into a components and expressing a force as a Cartesian vector will be use to solve problems involving the equilibrium of a particle. Since the dimensions or size of a particle are assumed to be neglected, therefore a particle can be subjected only to a system of concurrent forces.
Condition for Equilibrium of a particle
The condition for a particle equilibrium is based upon a balance of force. Formally stated as Newton’s first law of motion: If the resultant force acting on a particle is zero, then the particle is in equilibrium. Hence, the equilibrium requires that a particle either be at rest or move with constant velocity.
The above condition for particle equilibrium may be stated mathematically as
S F = 0 (3)
The Free-Body Diagram
The following three steps are necessary to construct a free-body diagram.
1. Isolate the particle from its surroundings by drawing (sketching) an outlined shape of the particle.
2. Indicate on this sketch all the forces that act on the particle.
3. The forces that are known should be labeled with proper magnitude and direction. Letters are used to represent the magnitudes and direction angles of forces that are unknown.
(If a force has a known line of action but unknown magnitude, the “arrowhead,” which define the direction sense of the force, can be assumed. The correctness of the directional sense will become apparent after solving the equilibrium equations for the unknown magnitude. If the solution yields a “negative” magnitude, the minus sign indicates that the arrowhead or directional sense of the force is opposite to that which was originally assumed).
|
|
|
|
|
|
* Cables and Pulleys
|
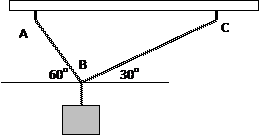
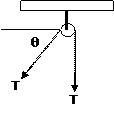
All cables are assumed to have negligible weight and they cannot be stretched. A cable can support only a tension or “pulling” force, and this force always acts in the direction of the cable. From the figure, for any angle q, the cable is subjected to a constant tension T through its length.
|
|
* Mass and weight
The mass of a body is an absolute quantity since its measurement can be made at any location. The weight of a body, however, is not absolute since its measured in a gravitational field, and hence its magnitude depends upon where the measurement is made.
In the SI system the mass of the body is specified in kg and the weight must be calculated using the equation F = ma. Hence, if a body has a mass of m(kg) and is located a point where the acceleration due to gravity is g(m/s2), then the weight is expressed in newtons as W = mg (N). In particular, if the body is located on the earth at sea level and at a latitude of 45o, the acceleration due to gravity is g= 9.80665 m/s2, For calculations, the value g = 9.81 m/s2 will be used so that
W = mg (N) (g = 9.81 m/s2)
Therefore, a body of mass 1 kg has a weight of 9.81 N.
Coplanar Force System
Many particle equilibrium problems involve a coplanar force system. If the forces lie in the x-y plane, they can each be resolved into their respective i and j components and the equilibrium equation can be written as
S F = 0
S Fxi + S Fy j = 0
For this vector equation to be satisfied, the x and y components must each equal zero, i.e.,
S Fx = 0
S Fy = 0
These scalar equilibrium equations require that the algebraic sum of the x and y components of all the forces acting on the particle be equal to zero.
Three-Dimensional Force System
The particle equilibrium requires
S F = 0
If the forces acting on the particle are resolved into i, j, k (or x, y, z) components, then we can write
S Fxi + S Fy j + S Fz k = 0
which requires that the following three scalar component equation be satisfied:
S Fx = 0
S Fy = 0
S Fz = 0
Using the above equations we can solve for at most three unknowns, generally represented as angles or magnitudes of forces shown on the free body diagram of the particle.