السرعة (4) - ملحق
Velocity (Appendix)

السيارة والسرعة
السرعة النسبية	عجلة سقوط الجسم الفعلية
الأجزاء: (1) (2) (3) 4

السرعة النسبية relative velocity:

تعرف السرعة النسبية بأنها الفرق بين سرعة جسمين: سرعة جسم بالنسبة للأخر كما لوكان غير متحرك. بحيث:

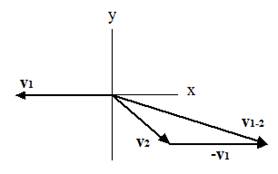
v_1-2 = v₁ – v₂

تستخدم المعادلة لحساب السرعة النسبية v_1-2 بين سرعة الجسم 1 (v₁) و سرعة الجسم 2 (v₂).

السرعة النسبية في البعد الواحد (نفس الاتجاه): يستخدم الجمع الجبري لمقدار السرعة speed.
والسرعة النسبية في بعدين أو أكثر يتم عن طريق جمع المتجاهات للسرعتين.

وتستخدم السرعة النسبية في العديد من التطبيقات ومنها الطيران بصفة خاصة:

تطبيقات الطائرة:
يعتمد رفع ديناميكا الهواء aerodynamic lift على قيمة مربع السرعة بين الطائرة والهواء (السرعة النسبية). حيث تأثير الرفع لا يتأثر فقط بسرعة الطائرة في الهواء ولكنه يتأثر أيضا بسرعة الهواء. ولوصف السرعة النسبية يجب اختيار مرجع ثابت للقياس (نقطة ثابتة للقياس) fixed reference وقياس السرعة بالنسبة لهذا النقطة الثابتة. وقد تكون تلك النقطة هي الأرض. وهنا يجب معرفة العلاقة بين سرعة الرياح wind speed إلى السرعة الأرضية للطائرة (السرعة بالنسبة للأرض)ground speed و سرعة الطائرة بالنسبة للهواءairspeed .

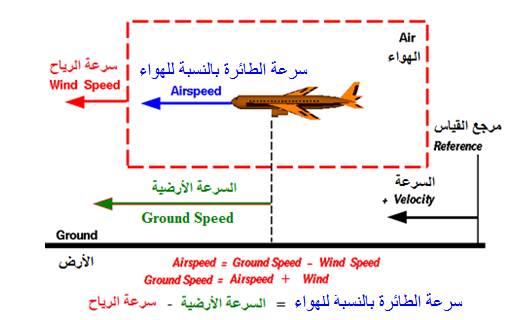
- سرعة الرياح wind speed:
سرعة الرياح تعتبر كمية متجه ويكون لها مقدار واتجاه, سرعة الرياح في اتجاه الطائرة تكون موجبة مع اتجاه حركة الطائرة. ولحساب السرعة النسبية بين سرعة الرياح وسرعة الطائرة سوف يهمل سرعة الرياح في الاتجاهات الأخرى, وهي السرعة الجانبية والتي يكون فيها اتجاه الهواء عمودي على الطائرة cross winds وكذلك سرعة رفع أو خفض الطائرة والتي يكون فيها الهواء عمودي على الأرض updrafts and downdrafts.

- السرعة الأرضية (سرعة الطائر بالنسبة للأرض) ground speed:
ينسب سرعة الطائرة إلى نقطة ثابتة على الارض. وهي سرعة الطائرة بالنسبة لمراقب من الارض.

- سرعة الطائرة بالنسبة للهواء airspeed:
وهي مهمة لتوليد قوة رفع الطائرة, والتي تعتمد على مربع السرعة النسبية بين الطائرة والهواء. سرعة الطائرة لا يمكن قياسها مباشرة من الأرض, ولكن يجب حسابها من سرعة الارض وسرعة الرياح. سرعة الطائرة النسبية هي الفرق في السرعة بين السرعة الأرضية وسرعة الرياح.

سرعة الطائرة بالنسبة للهواء = السرعة الأرضية – سرعة الرياح

ومن المعادلة السابقة نرى أنه في الأيام التي يكون الهواء راكد (لا توجد حركة رياح), تكون السرعة النسبية للطائرة هي نفسها السرعة الأرضية.
في حالة أن الرياح تهب في نفس اتجاه حركة الطائرة (رياح خلفية tailwind), فتكون سرعة الطائرة النسبية أقل من السرعة الأرضية.
في حالة أن الرياح تهب في عكس اتجاه الطائرة (رياح أمامية headwind), فتكون سرعة الطائرة النسبية أعلى من السرعة الأرضية.

مثال:
أ- طائرة ساكنة على أرض المطار وتواجه رياح بسرعة 30 كم/ساعة في مواجهة الطائرة headwind. تكون سرعة الطائرة بالنسبة للهواء كالتالي:

سرعة الطائرة بالنسبة للهواء = السرعة الأرضية – سرعة الرياح
= 0 – (- 30) = 30 كم/ساعة

ب- طائرة تحتاج إلى 160 كم/ساعة للإقلاع (سرعة الطائرة بالنسبة للهواء). وتواجه رياح بسرعة 30 كم/ساعة في اتجاه مواجه للطائرة, هل ستقلع الطائرة إذا كانت سرعة الطائرة الأرضية = 130 كم/ساعة.

سرعة الطائرة بالنسبة للهواء = السرعة الأرضية – سرعة الرياح
= 130 – (- 30) = 160 كم/ساعة

إذا ستقلع الطائرة.

جـ- طائرة تحتاج إلى 160 كم/ساعة للإقلاع (سرعة الطائرة بالنسبة للهواء). وتواجه رياح بسرعة 30 كم/ساعة في اتجاه خلفي للطائرة, هل ستقلع الطائرة إذا كانت سرعة الطائرة الأرضية = 130 كم/ساعة.

سرعة الطائرة بالنسبة للهواء = السرعة الارضية – سرعة الرياح

= 130 – (30) = 100 كم/ساعة

إذا الطائرة لن تقلع.

تطبيقات أخرى للسرعة النسبية:

النفق الهوائي wind tunnel: اختبار مقاومة الهواء للسيارات, الطائرات.. يصنع نموذج بنسبة معينه, ويثبت النموذج أو الجسم بالنفق الهوائي وتكون سرعة الرياح المولدة سالبة (مواجهة للنموذج). سواء كان النموذج هو المتحرك أو كان الهواء هو المتحرك فإن القوة المؤثرة على النموذج تكون هي نفسها.
تطيير الطائرة الورقية flying a kite: حيث أن الطائرة الورقية تكون مربوطة بخيط فإن السرعة الأرضية لها تكون مساوية للصفر. ولكنها تطير حيث أن الطائرة الورقية تكون لها سرعة بالنسبة للهواء مساوية لسرعة الرياح. يمكنك تطيير الطائر الورقية عندما يكون الهواء يهب عليك من الخلف.
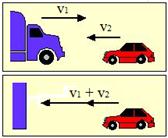
اصطدام السيارة بسيارة مقابلة head-on collision: عند اصطدام سيارة بسيارة مقابلة في الاتجاه المعاكس تكون سرعة التصادم هي السرعة النسبية بين السيارتان: سرعة التصادم = سرعة السيارة 1 – سرعة السيارة 2 v = v1 – (-v2) = v1 + v2 كمثل اصطدام السيارة بحاجز ثابت بسرعة مساوية لمجموع السرعتين.
مقاومة الهواء للسيارة أو الطائرة AR air (wind) resistance: تعتمد مقاومة الهواء على عدة عوامل: كثافة الهواء ρ, مساحة المواجهة A, ومعامل مقاومة الهواء Cd, والسرعة النسبية (التصادمية) بين الهواء والسيارةvwind v = vcar ±. السير عكس اتجاه الهواء يزيد من مقاومة الهواء ويزيد من استهلاك البنزين, والعكس صحيح. عند السير بسيارة حيث عدد السرعة يقرأ 80 كم/ساعة vcar, وهناك رياح مواجه بسرعة 20 كم/ساعة vwind) فإن سرعة السيارة بالنسبة للهواء تكون 100 كم/ساعة v .
تموين الطائرات في الجو بالوقود aerial refueling: تحتاج الطائرات للتموين بالوقود بالجو, وذلك لزيادة مدى طيران الطائرة. وكذلك تسهيل عملية الإقلاع بتقليل وزن الطائرة من الوقود, أو الاستفادة من تقليل الوزن بتحميل بضاعة بدلا عن الوقود. ولكي تتم عملية التموين بالوقود بالجو يجب أن تكون سرعة الطائرتان متساوية أي أن السرعة النسبية بينهما تكون صفر.
سرقة القطارات باستخدام الحصان train robbery: للتمكن من سرقة القطارات قديما أثناء سيرها, استخدم اللصوص الحصان في العدو خلف القطار حتى تصبح سرعة الحصان مساوية لسرعة القطار (السرعة النسبية بين الحصان والقطار تساوي صفر) وهنا يمكن للص الانتقال بسهولة من سرج الحصان إلى القطار.

أمثلة متحركة للسرعة النسبية:

An interactive version of this page is also available.
http://www.physicsclassroom.com/mmedia/vectors/plane.cfm

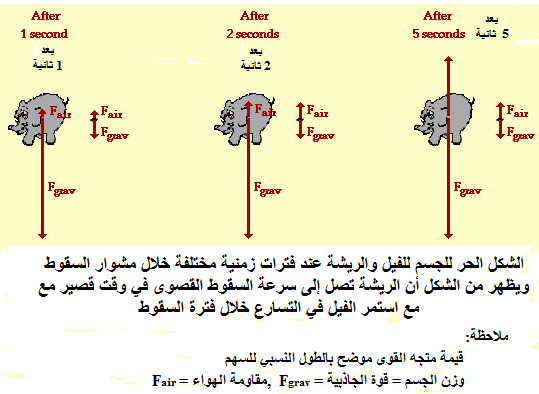
عجلة سقوط الجسم في حالة وجود مقاومة الهواء:

عند سقوط جسم في وجود الهواء فإن عجلة سقوط الجسم في لحظة بداية السقوط تكون مساوية لعجلة الجاذبية الأرضية ثم تقل مع مرور زمن السقوط حتى تصل إلى الصفر (في حالة مسافة السقوط تسمح لعجلة الجسم للوصول إلى الصفر). وتكون معادلة القوة المؤثرة على الجسم كالتالي:

مجموع القوى المؤثرة على الجسم = قوة القصور الذاتي
F = m aΣ

لحظة بداية السقوط:
F = m aΣ
w = m a
m g = m a
g = a

استمرار السقوط:
 F = m aΣ
 w – AR = m a

وحيث أن: الوزن = الكتلة × عجلة الجاذبية الأرضية (w = m g)  فتكون المعادلة:

m g – AR = m a

  g – (AR/m) = a

الوصول للسرعة القصوى للسقوط (مقاومة الهواء = وزن الجسم):
F = m aΣ
 w – AR = m a
0 = m a
0 = a

عند السرعة القصوى للسقوط تتساوي g مع AR تصبح العجلة تساوي صفر.

السرعة القصوى للسقوط والتي عندها عجلة الجسم تساوي صفر:

g – (AR/m) = 0

حيث أن مقاومة الهواء تساوي:

AR = ½ ρ A C_d v²

فتصبح المعادلة:

g - (1/2 ρ A C_d V²_termianl / m ) = 0

وتكون:

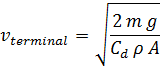
حيث:
m = كتلة الجسم (kg)
a = عجلة سقوط الجسم (m/s²)
g = عجلة الجاذبية الأرضية (9.81 m/s²)
AR = مقاومة الهواء (N)
ρ = كثافة الهواء (kg/m³)
A = مساحة الجسم المواجه للهواء (m²)
C_d = معامل مقاومة الهواء  
v = سرعة هبوط  (سقوط) الجسم (m/s)
v_terminal = سرعة السقوط القصوى (m/s)

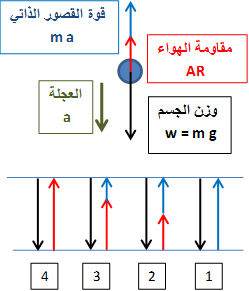
1- بداية سقوط الجسم: سرعة الجسم = صفر (مقاومة الهواء = صفر) عجلة الجسم = عجلة الجاذبية  الارضية 2- زيادة سرعة الجسم أدت إلى زيادة مقاومة الهواء. مع زيادة مقاومة الهواء قلت عجلة الجسم. 3- استمرار زيادة سرعة الجسم وزيادة مقاومة الهواء. مع استمرار زيادة مقاومة الهواء تتضاءل عجلة الجسم. 4- وصول سرعة الجسم  إلى السرعة القصوى للسقوط, والتي عندها مقاومة الهواء تساوي وزن الجسم, وتكون عجلة الجسم تساوي صفر. استمرار حركة الجسم بسرعة ثابتة تساوي السرعة القصوى للسقوط (عندها تكون العجلة تساوي صفر, وتكون سرعة الجسم ثابتة) حتى الانتهاء من السقوط.

حيث أن مقاومة الهواء تزيد مع السرعة, فإن ذلك سوف يؤدي إلى أن عجلة الجسم أثناء السقوط سوف تقل مع زيادة مسافة وزمن السقوط. حيث أن قيمة عجلة الجسم أثناء السقوط تبدأ بقيمة تساوي g  في بداية السقوط (عندها السرعة = 0) وتقل قيمة العجلة مع استمرار السقوط وزيادة السرعة وزيادة مقاومة الهواء, وتستمر قيمة العجلة في الانخفاض حتى تصل إلى 0 (عندها السرعة = سرعة السقوط القصوى) وذلك بناء على مسافة السقوط وشكل الجسم وأبعاده. ثم يستمر سقوط الجسم بعد ذلك بسرعة ثابتة (السرعة القصوى للسقوط).

حالة التسارع في حالة وجود الهواء:
يختلف التسارع مع اختلاف (الكتلة m, والمساحة A, ومعامل مقاومة الهواء C_d). هذا يعني أن الجسم الذي تقل نسبة m/(C_d A) عن الجسم الأخر يصل إلى سرعة الهبوط القصوى اسرع من الجسم الثاني وبذلك عند الوصول إلى تلك السرعة يستمر الجسم ذو النسبة الأقل بالهبوط بسرعة منتظمة بينما يظل الجسم الأخر بالتسارع مما يعني هبوط الجسم ذو النسبة m/(C_d A) الأعلى أسرع من الجسم الأخر.

حالة سقوط ريشة وفيل: نفترض سقوط فيل وريشة من مبنى مرتفع, من نفس الارتفاع وفي نفس الوقت. وخلال الحالة الفعلية سوف يواجه كلا من الفيل والريشة مقاومة للهواء. السؤال الأن: أي من الجسمين- الفيل أو الريشة- سوف يصل إلى الأرض أولا؟ معظم الناس لن يندهشوا من وصول الفيل للأرض أولا قبل الريشة. ولكن لماذا الفيل أسرع؟ الرد على هذا السؤال يكشف العديد من المغالطات وعدم الفهم وخلط الحقائق. الخلط يحدث من عدم فهم أو استيعاب معنى الوزن, قوة الجاذبية, التعجيل, مقاومة الهواء, سرعة السقوط القصوى.

الفيل والريشة يتم جذبهما لأسفل بواسطة قوة الجاذبية. عند بداية السقوط فإن قوة السقوط تكون غير متزنة. مع سقوط الجسمين يبدأن بالتسارع (اكتساب سرعة). مع اكتساب الجسمين سرعة, يواجه الجسمين قوة مقاومة الهواء لأعلى. حيث أن مقاومة الهواء تعتمد على سرعة سقوط الجسم ومساحة الجسم ومعامل الشكل لمقاومة الهواء وكثافة الهواء. بناء على مساحة الجسم فقط فإنه عند نفس السرعة فإن الفيل سوف يواجه مقاومة هواء أكبر من مقاومة الريشة.

ولكن لماذا الفيل الذي يواجه مقاومة هواء أكبر من الريشة يسقط أسرع؟ حيث أننا نعلم أن مقاومة الهواء تعمل على أبطاء سقوط الجسم لأسفل, والجسم ذو المقاومة الأكبر سيسقط أبطئ.

الإجابة على تلك التساؤلات يحتاج إلى فهم القانون الأول والثاني لنيوتن ومفهوم السرعة القصوى للسقوط. بناء على القانون الأول لنيوتن فإن الجسم سوف يحدث له تعجيل في حالة أن القوى المؤثرة عليه تكون غير متزنة. وأن مقدار التعجيل (التسارع) يتناسب طرديا مع مقدار محصلة القوى (القوى الغير متزنة) المؤثرة عليه. ولكن مع زيادة سرعة الجسم الساقط, فإنه يواجه زيادة في القوى المؤثرة لأعلى (قوة مقاومة الهواء). والحقيقة, أن الجسم سوف يستمر في التسارع (اكتساب سرعة) حتى تصل قيمة مقاومة الهواء لقيمة عالية كافية لتتزن مع قوة الجاذبية لأسفل (الوزن). وحيث أن الفيل له كتلة أكبر, فيكون وزنه أكبر ويتعرض لقوة جذب عالية لأسفل. وعليه فإن الفيل سوف يتسارع (تزداد سرعته) لمدة أطول من الوقت قبل تصبح قوة مقاومة الهواء لأعلى كافية لتتزن مع القوة الكبيرة للجذب لأسفل.

عندما تزيد قوة مقاومة الهواء لأعلى المؤثرة على الجسم بدرجة كافية لتتزن (تتعادل) مع قوة الجاذبية لأسفل, فإنه يقال أن الجسم وصل إلى السرعة القصوى للسقوط (حالة اتزان القوى). السرعة القصوى لسقوط الجسم هي السرعة الثابتة التي سيظل الجسم عليها حتى يصل إلى الأرض. في حالة الفيل والريشة, فإن الفيل سيكون له سرعة سقوط قصوى أعلى من الريشة. وكما ذكر من قبل, فإن الفيل ستظل سرعته بالزيادة لمدة أطول من الوقت. يحتاج الفيل إلى سرعة عالية ليحصل على قوة مقاومة الهواء لأعلى كافية لتتزن مع قوة الجاذبية لأسفل. والحقيقة فإن سرعة سقوط الفيل قد لا تصل إلى السرعة القصوى خلال السقوط (تعتمد على مسافة وزمن السقوط). ونظرا لخف وزن الريشة فإنها تصل في وقت قصير إلى السرعة القصوى, وسوف تستمر بها خلال سقوطها بعد ذلك حتى تصل إلى الأرض.

وتكون النتيجة النهائية أن الفيل سوف يصل أسرع من الريشة عند سقوطهما من نفس الارتفاع.

ولكن في حالة عدم وجود هواء (حالة افتراضية), فإن الريشة والفيل سيصلان الأرض في نفس الوقت.

http://www.physicsclassroom.com/mmedia/newtlaws/efar.cfm

الجزء الأول 1
الجزء الثاني 2
الجزء الثالث 3
الجزء الرابع 4